Question

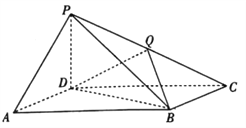
【题目】如图，扇形AOB，圆心角AOB等于60°，半径为2，在弧AB上有一动点P，过P引平行于OB的直线和OA交于点C，设∠AOP＝θ，求△POC面积的最大值及此时θ的值.

Answer 1

【答案】.

【解析】

根据CP∥OB求得∠CPO和和∠OCP，进而在△POC中利用正弦定理求得PC和OC，进而利用三角形面积公式表示出S（θ），利用两角和公式化简整理后，利用θ的范围确定三角形面积的最大值．

因为CP∥OB，所以∠CPO＝∠POB＝60°﹣θ，∴∠OCP＝120°．

在△POC中，由正弦定理得

，∴，所以CPsinθ．

又，∴OCsin（60°﹣θ）．

因此△POC的面积为

S（θ）CPOCsin120°sinθsin（60°﹣θ）

sinθsin（60°﹣θ）sinθ（cosθsinθ）

（sinθcosθsin2θ）

（sin2θcos2θ）

[cos（2θ﹣60°）]，θ∈（0°，60°）．

所以当θ＝30°时，S（θ）取得最大值为．