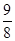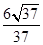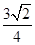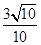题目内容
设圆(x+1)2+y2=25的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( )
A. - -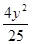 =1 =1 | B. + +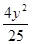 =1 =1 |
C.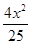 - - =1 =1 | D.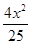 + + =1 =1 |
D
解析

练习册系列答案
相关题目
已知曲线 :
: 和
和 :
: 的焦点分别为
的焦点分别为 、
、 ,点
,点 是
是 和
和 的一个交点,则△
的一个交点,则△ 的形状是( )
的形状是( )
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.都有可能 |
已知 为椭圆
为椭圆 的两个焦点,过
的两个焦点,过 的直线交椭圆于两点,
的直线交椭圆于两点, ,
,
则 ( )
( )
A. | B. | C. | D. |
抛物线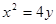 的焦点坐标是( )
的焦点坐标是( )
A. | B. | C. | D. |
已知双曲线中心在原点且一个焦点为F1(- ,0),点P位于该双曲线上,线段PF1的中点坐标为(0,2),则双曲线的方程是( )
,0),点P位于该双曲线上,线段PF1的中点坐标为(0,2),则双曲线的方程是( )
A. -y2=1 -y2=1 | B.x2- =1 =1 |
C. - - =1 =1 | D. - - =1 =1 |
如图,F为抛物线y2=4x的焦点,A,B,C在抛物线上,若 +
+ +
+ =0,则|
=0,则| |+|
|+| |+|
|+| |=( )
|=( )
| A.6 | B.4 | C.3 | D.2 |
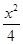 +y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,则点P的横坐标为( )
+y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,则点P的横坐标为( )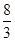

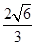
 -
- =1(a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7∶5的两段,则此双曲线的离心率为( )
=1(a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7∶5的两段,则此双曲线的离心率为( )