题目内容
若函数f（arcsinx）=x-1，则f(| π | 3 |
分析：由题意已知函数f（arcsinx）=x-1，利用换元法先求出函数的解析式，再利用解析式代入求值即可．
解答：解：由于函数f（arcsinx）=x-1，令t=arcsinx，则x=sint，所以函数f（arcsinx）=x-1??f（t）=sint-1，所以f(
)=sin
-1=
-1．
故答案为：
-1．
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：此题考查了换元法求函数解析，还考查了有解析式代入求函数值．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
=________．
= ．
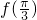