Question

正四面体ABCD中，AB与平面BCD所成角的正弦值为（　　）

• A、

  6

  3

• B、

  3

  6

• C、

  2

  4

• D、

  3

  3

Answer 1

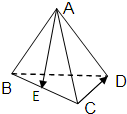
分析：在正四面体ABCD中，过A作AH⊥平面BCD于点H，则H为底面正三角形BCD的外心，连接BH，则∠ABH=α，就是AB与平面BCD所成角，解直角三角形ABH即可．

解答：解：正四面体ABCD，高为AH，
则H为底面正三角形BCD的外心，则∠ABH=α，就是AB与平面BCD所成角，
在Rt△ABH中，设棱长为a，
则BH=a

3

2

×

2

3

=

3

3

a，AH=

a2-( 3 3 )2

=

6

3

a，
∴sinα=

AH

AB

=

6 a 3

a

=

6

3

故选A．

点评：考查直线和平面所成的角，关键是找到斜线在平面内的射影，把空间角转化为平面角求解，属基础题．