题目内容
20. 若P、Q、R是边长为1的正△ABC边BC上的四等分点,则$\overrightarrow{AB}$•$\overrightarrow{AP}$+$\overrightarrow{AP}$•$\overrightarrow{AQ}$+$\overrightarrow{AQ}$•$\overrightarrow{AR}$+$\overrightarrow{AR}$•$\overrightarrow{AC}$=$\frac{13}{4}$.
若P、Q、R是边长为1的正△ABC边BC上的四等分点,则$\overrightarrow{AB}$•$\overrightarrow{AP}$+$\overrightarrow{AP}$•$\overrightarrow{AQ}$+$\overrightarrow{AQ}$•$\overrightarrow{AR}$+$\overrightarrow{AR}$•$\overrightarrow{AC}$=$\frac{13}{4}$.
分析 由题意建立平面直角坐标系,求出所用点的坐标,得到向量的坐标,由数量积的坐标运算得答案.
解答 解:建立如图所示平面直角坐标系,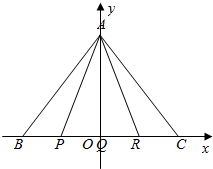
∵P、Q、R是边长为1的正△ABC边BC上的四等分点,
∴Q(0,0),R($\frac{1}{4},0$),C($\frac{1}{2},0$),P($-\frac{1}{4},0$),B($-\frac{1}{2},0$),A(0,$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{AB}$•$\overrightarrow{AP}$+$\overrightarrow{AP}$•$\overrightarrow{AQ}$+$\overrightarrow{AQ}$•$\overrightarrow{AR}$+$\overrightarrow{AR}$•$\overrightarrow{AC}$=2($\overrightarrow{AB}$•$\overrightarrow{AP}$+$\overrightarrow{AP}$•$\overrightarrow{AQ}$)
=2[($-\frac{1}{2},-\frac{\sqrt{3}}{2}$)($-\frac{1}{4},-\frac{\sqrt{3}}{2}$)+($-\frac{1}{4},-\frac{\sqrt{3}}{2}$)(0,$-\frac{\sqrt{3}}{2}$)]
=2($\frac{1}{8}+\frac{3}{4}+\frac{3}{4}$)=$\frac{13}{4}$.
故答案为:$\frac{13}{4}$.
点评 本题考查平面向量的数量积运算,建立平面直角坐标系使该题起到事半功倍的效果,是中档题.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
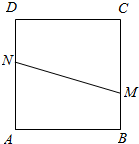 如图,边长为1正方形ABCD中,分别在边BC、AD上各取一点M与N,下面用随机模拟的方法计算|MN|>1.1的概率.利用计算机中的随机函数产生两个0~1之间的随机实数x,y,设BM=x,AN=y,则可确定M、N点的位置,进而计算线段MN的长度.设x,y组成数对(x,y),经随机模拟产生了20组随机数:
如图,边长为1正方形ABCD中,分别在边BC、AD上各取一点M与N,下面用随机模拟的方法计算|MN|>1.1的概率.利用计算机中的随机函数产生两个0~1之间的随机实数x,y,设BM=x,AN=y,则可确定M、N点的位置,进而计算线段MN的长度.设x,y组成数对(x,y),经随机模拟产生了20组随机数: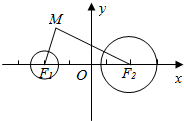 如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:(x-5)2+y2=16,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.
如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:(x-5)2+y2=16,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.