题目内容
10.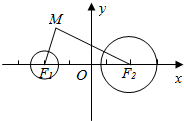 如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:(x-5)2+y2=16,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.
如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:(x-5)2+y2=16,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.
分析 根据两圆外切的充要条件转化为双曲线的定义求解.
解答 解:圆F1:x2+y2+10x+24=0可化为(x+5)2+y2=1,
圆F2:(x-5)2+y2=42,
∴F1(-5,0),半径r1=1;F2(5,0),半径r2=4.
设动圆M的半径为R,则|MF1|=R+1,|MF2|=R+4,
∴|MF2|-|MF1|=3<|F1F2|=10.
∴M点的轨迹是以F1、F2为焦点的双曲线左支,且a=$\frac{3}{2}$,c=5,
∴b2=25-$\frac{9}{4}=\frac{91}{4}$.
∴动圆圆心M的轨迹方程为$\frac{4{x}^{2}}{9}-\frac{4{y}^{2}}{91}$=1(x≤-$\frac{3}{2}$).
点评 本题考查轨迹方程的求法,该题将相切问题转化为动点到两定点的距离问题,应联想能运用圆锥曲线的定义求解,是中档题.

练习册系列答案
相关题目
20.抛物线y2=2px(p>0)的弦PQ的中点为(x0,y0)(y0≠0),则弦PQ的斜率是( )
| A. | $\frac{p}{{y}_{0}}$ | B. | -$\frac{p}{{y}_{0}}$ | C. | px0 | D. | -px0 |
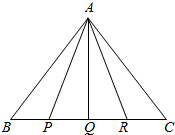 若P、Q、R是边长为1的正△ABC边BC上的四等分点,则$\overrightarrow{AB}$•$\overrightarrow{AP}$+$\overrightarrow{AP}$•$\overrightarrow{AQ}$+$\overrightarrow{AQ}$•$\overrightarrow{AR}$+$\overrightarrow{AR}$•$\overrightarrow{AC}$=$\frac{13}{4}$.
若P、Q、R是边长为1的正△ABC边BC上的四等分点,则$\overrightarrow{AB}$•$\overrightarrow{AP}$+$\overrightarrow{AP}$•$\overrightarrow{AQ}$+$\overrightarrow{AQ}$•$\overrightarrow{AR}$+$\overrightarrow{AR}$•$\overrightarrow{AC}$=$\frac{13}{4}$.