题目内容
已知函数f(x)=tan(2x+| π |
| 4 |
(1)求f(x)的定义域与最小正周期;
(2)设α∈(0,
| π |
| 4 |
| α |
| 2 |
分析:(Ⅰ)利用正切函数的定义域求出函数的定义域,利用周期公式求出最小正周期;
(Ⅱ)通过f(
)=2cos2α,化简表达式,结合α∈(0,
),求出α的大小.
(Ⅱ)通过f(
| α |
| 2 |
| π |
| 4 |
解答:解:(Ⅰ)由2x+
≠
+kπ,k∈Z.所以x≠
+
,k∈Z.所以f(x)的定义域为:x∈R|x≠
+
,k∈Zf(x)的最小正周期为:
.
(Ⅱ)由f(
)=2cos2α得tan(α+
)=2cos2α,
=2(cos2α-sin2α)
整理得
=2(cos α-sinα)(cosα+sinα) 因为α∈(0,
),所以sinα+cosα≠0 因此(cosα-sinα)2=
即sin2α=
因为α∈(0,
),
所以α=
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| kπ |
| 2 |
| π |
| 8 |
| kπ |
| 2 |
| π |
| 2 |
(Ⅱ)由f(
| α |
| 2 |
| π |
| 4 |
sin(α+
| ||
cos(α+
|
整理得
| sinα+cosα |
| cosα-sinα |
| π |
| 4 |
| 1 |
| 2 |
即sin2α=
| 1 |
| 2 |
| π |
| 4 |
所以α=
| π |
| 12 |
点评:本题考查两角和的正弦函数、余弦函数、正切函数公式,同角三角函数的基本关系式,二倍角公式等基本知识,考查基本运算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 -1)+lnx,t为常数,且t>0.
-1)+lnx,t为常数,且t>0.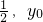 )处的切线方程为2x+y-2+ln2,求t和y0的值;
)处的切线方程为2x+y-2+ln2,求t和y0的值; -1)+lnx,t为常数,且t>0.
-1)+lnx,t为常数,且t>0. )处的切线方程为2x+y-2+ln2,求t和y的值;
)处的切线方程为2x+y-2+ln2,求t和y的值;