题目内容
若函数f(x)=logax(0<a<1)在区间[a,2a]上的最小值是最大值的 ,则a的值为( )
,则a的值为( )A.
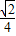
B.
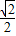
C.

D.

【答案】分析:由题意函数是减函数,由数f(x)=logax(0<a<1)在区间[a,2a]上的最小值是最大值的 ,建立方程求出a的值
,建立方程求出a的值
解答:解:由题意函数f(x)=logax(0<a<1)在区间[a,2a]上是减函数,
又数f(x)=logax(0<a<1)在区间[a,2a]上的最小值是最大值的 ,
,
∴loga2a= logaa=
logaa=
∴loga2=-
∴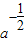 =2
=2
∴a=
故选C
点评:本题考查对数函数的单调性与特殊点,解题的关键是判断出函数的单调性确定出函数的最值,由此则可以利用最小值是最大值的 ,建立方程求出a
,建立方程求出a
 ,建立方程求出a的值
,建立方程求出a的值解答:解:由题意函数f(x)=logax(0<a<1)在区间[a,2a]上是减函数,
又数f(x)=logax(0<a<1)在区间[a,2a]上的最小值是最大值的
 ,
,∴loga2a=
 logaa=
logaa=
∴loga2=-

∴
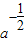 =2
=2∴a=

故选C
点评:本题考查对数函数的单调性与特殊点,解题的关键是判断出函数的单调性确定出函数的最值,由此则可以利用最小值是最大值的
 ,建立方程求出a
,建立方程求出a 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目