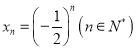题目内容
【题目】已知函数![]() ,
,![]() (
(![]() 且
且![]() )
)
(1)判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)当![]() 时,直接写出函数
时,直接写出函数![]() 的单调区间(不需证明)
的单调区间(不需证明)
(3)若![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)为偶函数,见解析;(2)单调增区间为![]() 单调减区间为
单调减区间为![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据题意,![]() ,先分析函数的定义域,进而可得
,先分析函数的定义域,进而可得![]() ,结合函数奇偶性的定义分析可得答案;
,结合函数奇偶性的定义分析可得答案;
(2)根据题意,![]() ,由复合函数单调性的判定方法分析可得答案;
,由复合函数单调性的判定方法分析可得答案;
(3)根据题意,若![]() ,即
,即![]() ,结合对数的运算性质分析可得答案.
,结合对数的运算性质分析可得答案.
(1)根据题意,函数![]() ,
,![]() ,
,
则![]() ,
,
必有![]() ,解可得
,解可得![]() ,即函数的定义域为
,即函数的定义域为![]() ;
;
又由![]() ,
,
则函数![]() 为偶函数;
为偶函数;
(2)根据题意,![]() ,
,
又由![]() ,其递增区间为
,其递增区间为![]() ,递减区间为
,递减区间为![]() ;
;
(3)根据题意,若![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,符合题意;
,符合题意;
当![]() 时,
时,![]() ,若
,若![]() ,即
,即![]() ,解可得:
,解可得:![]() ,
,
此时![]() 的取值范围
的取值范围![]() ,
,
综合可得:![]() 的取值范围为
的取值范围为![]() .
.

【题目】2019年某地区初中升学体育考试规定:考生必须参加长跑、掷实心球、1分钟跳绳三项测试.某学校在九年级上学期开始,就为掌握全年级学生1分钟跳绳情况,抽取了100名学生进行测试,得到下面的频率分布直方图.
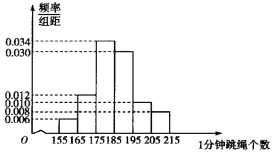
(Ⅰ)规定学生1分钟跳绳个数大于等于185为优秀.若在抽取的100名学生中,女生共有50人,男生1分钟跳绳个数大于等于185的有28人.根据已知条件完成下面的![]() 列联表,并根据这100名学生的测试成绩,判断能否有99%的把握认为学生1分钟跳绳成绩是否优秀与性别有关.
列联表,并根据这100名学生的测试成绩,判断能否有99%的把握认为学生1分钟跳绳成绩是否优秀与性别有关.
1分钟跳绳成绩 | 优秀 | 不优秀 | 合计 |
男生人数 | 28 | ||
女生人数 | 100 | ||
合计 | 100 |
(Ⅱ)根据往年经验,该校九年级学生经过训练,正式测试时每人1分钟跳绳个数都有明显进步.假设正式测试时每人1分钟跳绳个数都比九年级上学期开始时增加10个,全年级恰有2000名学生,若所有学生的1分钟跳绳个数![]() 服从正态分布
服从正态分布![]() ,用样本数据的平均值和标准差估计
,用样本数据的平均值和标准差估计![]() 和
和![]() ,各组数据用中点值代替),估计正式测试时1分钟跳绳个数大于183的人数(结果四舍五入到整数
,各组数据用中点值代替),估计正式测试时1分钟跳绳个数大于183的人数(结果四舍五入到整数
附: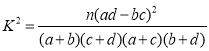 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]()
![]()
![]()