题目内容
【题目】已知函数![]() ,各项均不相等的数列
,各项均不相等的数列![]() 满足
满足![]()
![]() .令
.令![]() .给出下列三个命题:
.给出下列三个命题:
(1)存在不少于3项的数列![]() ,使得
,使得![]() ;
;
(2)若数列![]() 的通项公式为
的通项公式为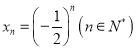 ,则
,则![]() 对
对![]() 恒成立;
恒成立;
(3)若数列![]() 是等差数列,则
是等差数列,则![]() 对
对![]() 恒成立.
恒成立.
其中真命题的序号是( )
A.(1)(2)B.(1)(3)C.(2)(3)D.(1)(2)(3)
【答案】D
【解析】
由题意得![]() 是奇函数,只需考查
是奇函数,只需考查![]() 时,
时,![]() 的奇偶性,而
的奇偶性,而![]() 和
和![]() 都在
都在![]() 上是增函数,所以
上是增函数,所以![]() 在
在![]() 上是增函数,即
上是增函数,即![]() 时,
时,![]()
对于(1),取![]() 即可判断;
即可判断;
对于(2),运用等比数列的求和公式和三角函数的性质,即可判断;
对于(3),运用等差数列的性质和函数的性质,以及不等式的性质,结合函数![]() 的单调性,即可判断.
的单调性,即可判断.
由题意得![]() ,所以
,所以![]() 是奇函数,只需考查
是奇函数,只需考查![]() 时,
时,![]() 的奇偶性,而
的奇偶性,而![]() 和
和![]() 都在
都在![]() 上是增函数,所以
上是增函数,所以![]() 在
在![]() 上是增函数;
上是增函数;
所以![]() 在
在![]() 上是增函数.设
上是增函数.设![]() ,
,
若![]() ,则
,则![]() 即
即![]() ,
,![]()
若![]() ,则
,则![]() 即
即![]() ,
,![]()
∴![]() 时,
时,![]()
对于(1),取![]() 则
则![]() 因此(1)正确;
因此(1)正确;
对于(2),∵ ,∴
,∴![]()

![]() ,
,
又![]() 时,
时,![]()
![]()
 ,
,
令![]() ,则
,则![]() ,
,
所以![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,所以
,所以![]() ,
,
又因为![]() ,
,
所以![]() ,即
,即![]() 对于
对于![]() 恒成立,故(2)正确;
恒成立,故(2)正确;
对于(3),因为数列![]() 是等差数列,若
是等差数列,若![]() ,
,
若![]() 则
则![]() ,可得
,可得![]() 相加即可得到
相加即可得到![]() ,所以
,所以![]()
若![]() 则
则![]() ,可得
,可得![]()
相加即可得到![]() ,所以
,所以![]()
故(3)正确.
故选:D.

 特高级教师点拨系列答案
特高级教师点拨系列答案【题目】2019年国际篮联篮球世界杯,将于2019年在的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传世界杯,某大学从全校学生中随机抽取了![]() 名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
会收看 | 不会收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根据上表说明,能否有![]() 的把握认为收看篮球世界杯赛事与性别有关?
的把握认为收看篮球世界杯赛事与性别有关?
(2)现从参与问卷调查且收看篮球世界杯赛事的学生中,采用按性别分层抽样的方法选取![]() 人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
(i)求男、女学生各选取多少人;
(ii)若从这![]() 人中随机选取
人中随机选取![]() 人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到
人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到![]() 名男生的概率.
名男生的概率.
附: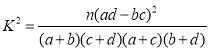 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|