题目内容
已知向量 =(cosx,sinx),
=(cosx,sinx), =
= ,且
,且 .
.求:(1)
 •
• 和|
和| -
- |的取值范围;
|的取值范围;(2)函数f(x)=
 •
• -|
-| -
- |的最小值.
|的最小值.
【答案】分析:(1)要求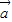 •
•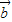 和|
和|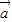 -
-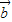 |的取值范围,我们要根据向量
|的取值范围,我们要根据向量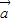 =(cosx,sinx),
=(cosx,sinx),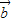 =
=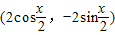 ,且
,且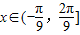 .将其转化为三角函数的值域问题,然后根据正弦型函数的性质进行求解.
.将其转化为三角函数的值域问题,然后根据正弦型函数的性质进行求解.
(2)由(1)的结论,我们易给出f(x)=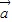 •
•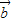 -|
-|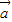 -
-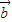 |的解析式,再根据正弦型函数最值的求法,即可得到f(x)=
|的解析式,再根据正弦型函数最值的求法,即可得到f(x)=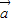 •
•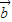 -|
-|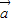 -
-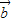 |的最小值.
|的最小值.
解答:解:(1)∵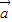 =(cosx,sinx),
=(cosx,sinx),
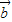 =
=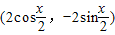
∴a•b=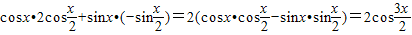
又∵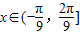 ,
,
∴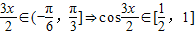
∴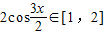 即
即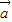 •
•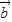 ∈[1,2]
∈[1,2]
∵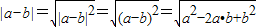
=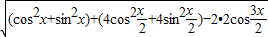
=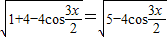
又∵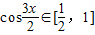 ∴
∴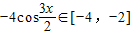
∴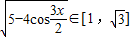 ;
;
(2)由(1)知:f(x)=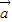 •
•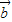 -|
-|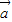 -
-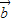 |=
|=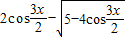
设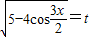 ,则
,则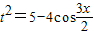 ,
,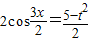
∴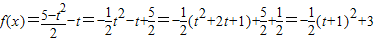
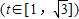
∴由图象可知:当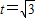 时,函数f(x)取得最小值
时,函数f(x)取得最小值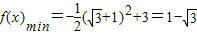 .
.
点评:函数y=Asin(ωx+φ)(A>0,ω>0)中,最大值或最小值由A确定,由周期由ω决定,即要求三角函数的周期与最值一般是要将其函数的解析式化为正弦型函数,再根据最大值为|A|,最小值为-|A|,周期T=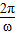 进行求解.如果求其在区间上的值域和最值,则要结合图象进行讨论.
进行求解.如果求其在区间上的值域和最值,则要结合图象进行讨论.
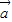 •
•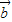 和|
和|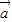 -
-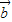 |的取值范围,我们要根据向量
|的取值范围,我们要根据向量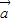 =(cosx,sinx),
=(cosx,sinx),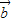 =
=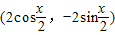 ,且
,且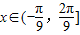 .将其转化为三角函数的值域问题,然后根据正弦型函数的性质进行求解.
.将其转化为三角函数的值域问题,然后根据正弦型函数的性质进行求解.(2)由(1)的结论,我们易给出f(x)=
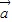 •
•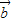 -|
-|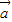 -
-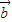 |的解析式,再根据正弦型函数最值的求法,即可得到f(x)=
|的解析式,再根据正弦型函数最值的求法,即可得到f(x)=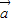 •
•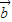 -|
-|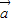 -
-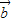 |的最小值.
|的最小值.解答:解:(1)∵
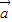 =(cosx,sinx),
=(cosx,sinx),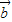 =
=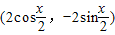
∴a•b=
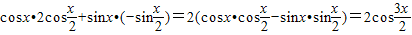
又∵
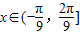 ,
,∴
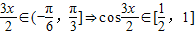
∴
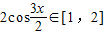 即
即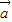 •
•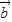 ∈[1,2]
∈[1,2]∵
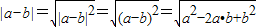
=
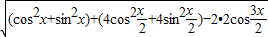
=
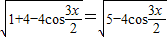
又∵
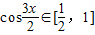 ∴
∴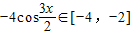
∴
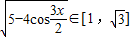 ;
;(2)由(1)知:f(x)=
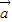 •
•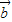 -|
-|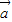 -
-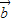 |=
|=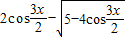
设
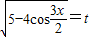 ,则
,则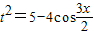 ,
,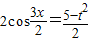
∴
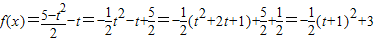
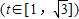
∴由图象可知:当
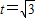 时,函数f(x)取得最小值
时,函数f(x)取得最小值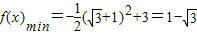 .
.点评:函数y=Asin(ωx+φ)(A>0,ω>0)中,最大值或最小值由A确定,由周期由ω决定,即要求三角函数的周期与最值一般是要将其函数的解析式化为正弦型函数,再根据最大值为|A|,最小值为-|A|,周期T=
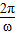 进行求解.如果求其在区间上的值域和最值,则要结合图象进行讨论.
进行求解.如果求其在区间上的值域和最值,则要结合图象进行讨论. 
练习册系列答案
相关题目