题目内容
7.已知函数f(x)=cos2x+$\sqrt{3}$sinxcosx.(Ⅰ)求函数f(x)的最小正周期及单调递增区间;
(Ⅱ)求f(x)在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上的最大值和最小值.
分析 (Ⅰ)利用二倍角和辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期,最后将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;
(Ⅱ)当x∈[-$\frac{π}{6}$,$\frac{π}{3}$]时,求出内层函数的取值范围,结合三角函数的图象和性质,可求出f(x)的最大值和最小值.
解答 解:(Ⅰ)已知函数函数f(x)=cos2x+$\sqrt{3}$sinxcosx.
化解可得:f(x)=$\frac{1}{2}+\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x=sin(2x$+\frac{π}{6}$)$+\frac{1}{2}$
∴函数f(x)的最小正周期T=$\frac{2π}{2}=π$
由$2kπ-\frac{π}{2}≤$2x$+\frac{π}{6}$$≤\frac{π}{2}+2kπ$,(k∈Z)
解得:$kπ-\frac{π}{3}$≤x≤$kπ+\frac{π}{3}$.
∴函数f(x)的单调递增区间为:[$kπ-\frac{π}{3}$,$kπ+\frac{π}{3}$],(k∈Z)
(Ⅱ)由(Ⅰ)知f(x)=sin(2x$+\frac{π}{6}$)$+\frac{1}{2}$
当x∈[-$\frac{π}{6}$,$\frac{π}{3}$]时,
可得:$-\frac{π}{6}$≤2x$+\frac{π}{6}$$≤\frac{5π}{6}$
所以$-\frac{1}{2}+\frac{1}{2}≤$sin(2x$+\frac{π}{6}$)$+\frac{1}{2}$$≤1+\frac{1}{2}$.即0≤f(x)$≤\frac{3}{2}$
故得f(x)在区间在[-$\frac{π}{6}$,$\frac{π}{3}$]上的最大值为$\frac{3}{2}$,最小值为0.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案| A. | 在[-π,π]上是增函数 | B. | 在[0,π]上是减函数 | ||
| C. | 在$[{-\frac{π}{2},\frac{π}{2}}]$上是减函数 | D. | 在[-π,0]上是减函数 |
| A. | b1b2…bn=b1b2…b17-n (n<17,n∈N*) | |
| B. | b1b2…bn=b1b2…b18-n(n<18,n∈N*) | |
| C. | b1+b2+…+bn=b1+b2+…+b17-n(n<17,n∈N*) | |
| D. | b1+b2+…+bn=b1+b2-1+…+b18-n(n<18,n∈N*) |
| 同一限定区域停车 | 不同一限定区域停车 | 合计 | |
| 男 | 5 | ||
| 女 | 10 | ||
| 合计 | 50 |
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握恩威是否同意限定区域停车与家长的性别有关?请说明理由.
附临界表及参考公式:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 函数f(x)=x2(x∈R)存在1级“理想区间” | |
| B. | 函数f(x)=ex(x∈R)不存在2级“理想区间” | |
| C. | 函数f(x)=$\frac{4x}{{x}^{2}+1}$(x≥0)存在3级“理想区间” | |
| D. | 函数f(x)=tanx,x∈(-$\frac{π}{2}$,$\frac{π}{2}$)不存在4级“理想区间” |
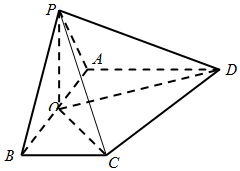 如图,已知在四棱锥P-ABCD中,O为AB中点,平面POC⊥平面ABCD,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3
如图,已知在四棱锥P-ABCD中,O为AB中点,平面POC⊥平面ABCD,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3