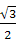题目内容
在三角形ABC中,BC=2,BC边上的高为 ,则∠BAC的范围为
,则∠BAC的范围为
- A.(0,
 ]
] - B.(0,
 ]
] - C.(0,
 ]
] - D.(0,
 ]
]
C
分析:设BC边的中垂线交直线L于A',作三角形A'BC的外接圆O,根据三角形外角定理,及圆周角定理的推论即可得到∠BAC的范围.
解答: 解:顶点A的轨迹是一条与BC边平行且到BC边距离为
解:顶点A的轨迹是一条与BC边平行且到BC边距离为 的直线L.
的直线L.
设BC边的中垂线交直线L于A',连接A'B,A'C.
三角形A'BC是等边三角形,且符合题设.则∠BA'C= .
.
作三角形A'BC的外接圆O.
在直线L上任取一点M,连接MB、MC.设MB与圆O交于N点,连接CN.
因为同弧上的圆周角相等,三角形外角大于不相邻的内角知:
∠BMC<∠BNC=∠BA'C=
所以∠BAC的取值范围是(0, ].
].
故选C
点评:本题考查的知识点是圆周角定理的推论及三角形外角的性质,其中作BC边的中垂线交直线L于A',作三角形A'BC的外接圆O,为圆周角定理的使用创造条件是解答本题的关键.
分析:设BC边的中垂线交直线L于A',作三角形A'BC的外接圆O,根据三角形外角定理,及圆周角定理的推论即可得到∠BAC的范围.
解答:
 解:顶点A的轨迹是一条与BC边平行且到BC边距离为
解:顶点A的轨迹是一条与BC边平行且到BC边距离为 的直线L.
的直线L.设BC边的中垂线交直线L于A',连接A'B,A'C.
三角形A'BC是等边三角形,且符合题设.则∠BA'C=
 .
.作三角形A'BC的外接圆O.
在直线L上任取一点M,连接MB、MC.设MB与圆O交于N点,连接CN.
因为同弧上的圆周角相等,三角形外角大于不相邻的内角知:
∠BMC<∠BNC=∠BA'C=

所以∠BAC的取值范围是(0,
 ].
].故选C
点评:本题考查的知识点是圆周角定理的推论及三角形外角的性质,其中作BC边的中垂线交直线L于A',作三角形A'BC的外接圆O,为圆周角定理的使用创造条件是解答本题的关键.

练习册系列答案
相关题目
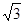 , 则AB+2BC的最大值为( )
, 则AB+2BC的最大值为( )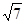 D.
2
D.
2 ,C=60
,C=60 B.
B.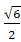 C.
C. D.
D.