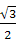题目内容
在三角形ABC中,B=60°,AC=
,则AB+2BC的最大值为( )
| 3 |
分析:设三角形的三边分别为a,b,c,利用余弦定理和已知条件求得a和c的关系,设c+2a=m代入,利用判别大于等于0求得m的范围,则m的最大值可得.
解答:解:由题意,设三角形的三边分别为a,b,c,则3=a2+c2-2accos60°
∴a2+c2-ac=3
设c+2a=m(m>0),代入上式得7a2-5am+m2-3=0
∴△=84-3m2≥0,∴0<m≤2
m=2
时,a=
,c=
符合题意
∴m的最大值是2
故选D.
∴a2+c2-ac=3
设c+2a=m(m>0),代入上式得7a2-5am+m2-3=0
∴△=84-3m2≥0,∴0<m≤2
| 7 |
m=2
| 7 |
5
| ||
| 7 |
4
| ||
| 7 |
∴m的最大值是2
| 7 |
故选D.
点评:本题考查余弦定理的运用,考查最值,考查学生的计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
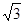 , 则AB+2BC的最大值为( )
, 则AB+2BC的最大值为( )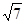 D.
2
D.
2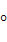 ,C=60
,C=60 B.
B.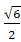 C.
C. D.
D.