题目内容
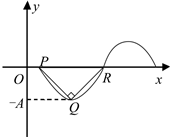 设函数f(x)=Acosωx(A>0,ω>0)的部分图象如图所示,其中△PQR为等腰直角三角形,∠PQR=
设函数f(x)=Acosωx(A>0,ω>0)的部分图象如图所示,其中△PQR为等腰直角三角形,∠PQR= ,PR=1.求:
,PR=1.求:
(1)函数f(x)的解析式;
(2)函数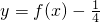 在x∈[0,10]时的所有零点之和.
在x∈[0,10]时的所有零点之和.
解:(1)由已知PR=1,
∴T=2= ,∴ω=π
,∴ω=π
∵△PQR为等腰直角三角形,
∴Q到x轴的距离即为A=
∴ ;
;
(2)由 ,得
,得 ,故
,故 或
或 (k∈Z),
(k∈Z),
所以当x∈[0,10]时的所有零点之和为 .
.
分析:(1)先利用函数图象确定函数的周期,从而确定ω的值,再利用△PQR为等腰直角三角形,求得函数f(x)的振幅A,从而确定函数解析式;
(2)先解方程f(x)= ,得
,得 或
或 (k∈Z),再令k=0,1,2,3,4,即可得x∈[0,10]时的所有零点,求和即可
(k∈Z),再令k=0,1,2,3,4,即可得x∈[0,10]时的所有零点,求和即可
点评:本题主要考查了y=Asin(ωx+φ)型函数的图象和性质,由其部分函数图象,求参数值的方法和技巧,简单的三角方程的解法,属基础题
∴T=2=
 ,∴ω=π
,∴ω=π∵△PQR为等腰直角三角形,
∴Q到x轴的距离即为A=

∴
 ;
; (2)由
 ,得
,得 ,故
,故 或
或 (k∈Z),
(k∈Z),所以当x∈[0,10]时的所有零点之和为
 .
.分析:(1)先利用函数图象确定函数的周期,从而确定ω的值,再利用△PQR为等腰直角三角形,求得函数f(x)的振幅A,从而确定函数解析式;
(2)先解方程f(x)=
 ,得
,得 或
或 (k∈Z),再令k=0,1,2,3,4,即可得x∈[0,10]时的所有零点,求和即可
(k∈Z),再令k=0,1,2,3,4,即可得x∈[0,10]时的所有零点,求和即可点评:本题主要考查了y=Asin(ωx+φ)型函数的图象和性质,由其部分函数图象,求参数值的方法和技巧,简单的三角方程的解法,属基础题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设函数f(x)=ax2+c(a≠0),若
f(x)dx=f(x0)0≤x0≤1,则x0的值为( )
| ∫ | 1 0 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 短长度为
短长度为 选考题
选考题