题目内容
某企业生产 两种产品,每生产
两种产品,每生产 吨产品所需的劳动力、煤、电消耗及利润如下表:
吨产品所需的劳动力、煤、电消耗及利润如下表:
因条件限制,该企业仅有劳动力 个,煤
个,煤 吨,供电局最多供电
吨,供电局最多供电 千瓦时,试问该企业生产
千瓦时,试问该企业生产 两种产品各多少吨时能获得最大利润?并求最大利润.
两种产品各多少吨时能获得最大利润?并求最大利润.
 两种产品,每生产
两种产品,每生产 吨产品所需的劳动力、煤、电消耗及利润如下表:
吨产品所需的劳动力、煤、电消耗及利润如下表:| 产品品种 | 劳动力(个) | 煤(吨) | 电(千瓦时) | 利润(万元) |
 产品 产品 | 4 | 9 | 3 | 7 |
 产品 产品 | 5 | 4 | 10 | 12 |
 个,煤
个,煤 吨,供电局最多供电
吨,供电局最多供电 千瓦时,试问该企业生产
千瓦时,试问该企业生产 两种产品各多少吨时能获得最大利润?并求最大利润.
两种产品各多少吨时能获得最大利润?并求最大利润.生产 产品
产品 吨,
吨, 产品
产品 吨时能获得最大利润
吨时能获得最大利润 万元。
万元。
 产品
产品 吨,
吨, 产品
产品 吨时能获得最大利润
吨时能获得最大利润 万元。
万元。本试题主要是考查了线性规划问题中最优解的求解和运用。
解:设生产A 吨生产B
吨生产B  吨。。。。。。。。。。。。。。。。。。。。。。。。1分
吨。。。。。。。。。。。。。。。。。。。。。。。。1分
由题意: ,目标函数
,目标函数 ,上。。。。。。。。。。。。。。。。。。。。。5分
,上。。。。。。。。。。。。。。。。。。。。。5分
述不等式组表示的平面区域如图所示,阴影部分(含边界)即可行域。作直线 ,并作平行于直线
,并作平行于直线 的一组直线,与可行域相交,其中有一条直线经过可行域上的点M,且与直线
的一组直线,与可行域相交,其中有一条直线经过可行域上的点M,且与直线 的距离最大,其中M点是直线
的距离最大,其中M点是直线 和直线
和直线 的交点,………………………………………………………………7分
的交点,………………………………………………………………7分
图(略)。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。9分
解方程组 得
得 ,此时
,此时 (万元),当
(万元),当 时,
时, 最得最大值。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。11分
最得最大值。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。11分
答:该企业生产 产品
产品 吨,
吨, 产品
产品 吨时能获得最大利润
吨时能获得最大利润 万元。。。。。。。。。12分
万元。。。。。。。。。12分
解:设生产A
 吨生产B
吨生产B  吨。。。。。。。。。。。。。。。。。。。。。。。。1分
吨。。。。。。。。。。。。。。。。。。。。。。。。1分由题意:
 ,目标函数
,目标函数 ,上。。。。。。。。。。。。。。。。。。。。。5分
,上。。。。。。。。。。。。。。。。。。。。。5分述不等式组表示的平面区域如图所示,阴影部分(含边界)即可行域。作直线
 ,并作平行于直线
,并作平行于直线 的一组直线,与可行域相交,其中有一条直线经过可行域上的点M,且与直线
的一组直线,与可行域相交,其中有一条直线经过可行域上的点M,且与直线 的距离最大,其中M点是直线
的距离最大,其中M点是直线 和直线
和直线 的交点,………………………………………………………………7分
的交点,………………………………………………………………7分图(略)。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。9分
解方程组
 得
得 ,此时
,此时 (万元),当
(万元),当 时,
时, 最得最大值。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。11分
最得最大值。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。11分答:该企业生产
 产品
产品 吨,
吨, 产品
产品 吨时能获得最大利润
吨时能获得最大利润 万元。。。。。。。。。12分
万元。。。。。。。。。12分
练习册系列答案
相关题目
 满足条件
满足条件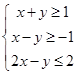 ,则目标函数
,则目标函数 的最大值是 .
的最大值是 .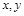 满足
满足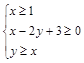 ,则
,则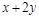 的最大值和最小值之和等于
的最大值和最小值之和等于 满足
满足 则
则 的最小值是 ;
的最小值是 ; ,则函数
,则函数 的最大值为_________ .
的最大值为_________ . 满足约束条件
满足约束条件 ,则
,则 的最大值为
的最大值为  ,则z=2|x|+y的取值范围是_________
,则z=2|x|+y的取值范围是_________ 的坐标满足
的坐标满足
 为坐标原点, 则
为坐标原点, 则 的最小值为( )
的最小值为( )


