题目内容

如图所示，矩形ABCD和矩形ABEF中，AF=AD，AM=DN，矩形ABEF可沿AB任意翻折.

（1）求证：当F、A、D不共线时，线段MN总平行于平面FAD；

（2）“不管怎样翻折矩形ABEF，线段MN总和线段FD平行.”这个结论对吗？如果对，请证明；如果不对，请说明能否改变个别已知条件使上述结论成立.

解析:（1）说明MN总平行于平面FAD的方法有两种，一是MN在一个总是与平面FAD平行的平面内；二是平面FAD内总有一条直线与MN平行.另外，对于折叠问题，要分析平面图形，搞清折叠前后量的变化.

（1）证明:在平面图形中，连结MN，设MN与AB交于点G.

    由于ABCD和ABEF都是矩形且AD=AF，从而有AD∥BE且AD=BE，

∴四边形ADBE是平行四边形.

    又AM=DN，根据比例关系得到MN∥AD.

    折叠之后，MG∥AF，NG∥AD，如右图∴平面ADF∥平面GNM.

    又MN平面GNM，∴MN∥平面ADF.

∴当F、A、D不共线时，MN总平行于平面ADF.

（2）解:这个结论不对.要使上述结论成立，M、N应为AE和DB的中点，由于平面MNG∥平面FDA，可知要使MN∥FD总成立，根据面面平行的性质定理，只要FD与MN共面即可.

    若要使FD与MN共面，连结FM，只要FM与DN相交即可.

    由平面图形知，若要DN和FM共面，应有DN与FM相交于点B，折叠后的图应使F、M、B三点共线即可.


练习册系列答案
相关题目
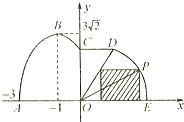精英家教网如图，某市拟在道路的一侧修建一条运动赛道，赛道的前一部分为曲线段ABC，该曲线段为函数y=Asin（ωx+φ）（A＞0，ω＞0，
π
2
＜φ＜π），x∈[-3，0]的图象，且图象的最高点为B（-1，3
2
）；赛道的中间部分为
3
千米的水平跑到CD；赛道的后一部分为以O圆心的一段圆弧
DE
．
（1）求ω，φ的值和∠DOE的值；
（2）若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”，如图所示，矩形的一边在道路AE上，一个顶点在扇形半径OD上．记∠POE=θ，求当“矩形草坪”的面积最大时θ的值．
如图所示，在△ABC中，AC=1，AB=3，∠ACB=
π2
，P为AB的中点且△ABC与矩形BCDE所在的平面互相垂直，CD=2．
（1）求证：AD∥平面PCE；
（2）求三棱锥P-ACE的高．
如图所示，在△ABC中，AC=1，AB=3，∠ACB=
π2
，P为AB的中点且△ABC与矩形BCDE所在的平面互相垂直，CD=2．
（1）求证：AD∥平面PCE；
（2）求二面角A-CE-P的余弦值．
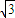如图，某市拟在道路的一侧修建一条运动赛道，赛道的前一部分为曲线段ABC，该曲线段为函数y=Asin（ωx+φ）（A＞0，ω＞0，＜φ＜π），x∈[-3，0]的图象，且图象的最高点为B（-1，3）；赛道的中间部分为千米的水平跑到CD；赛道的后一部分为以O圆心的一段圆弧．
（1）求ω，φ的值和∠DOE的值；
（2）若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”，如图所示，矩形的一边在道路AE上，一个顶点在扇形半径OD上．记∠POE=θ，求当“矩形草坪”的面积最大时θ的值．

（本小题满分14分）

如图，某市拟在道路的一侧修建一条运动赛道，赛道的前一部分为曲线段ABC，该曲线段为函数y＝(A＞0，＞0，＜＜)，x∈[－3，0]的图象，且图象的最高点为B(－1，)；赛道的中间部分为千米的水平跑到CD；赛道的后一部分为以O圆心的一段圆弧．

 （1）求，的值和∠DOE的值；

（2）若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”，如图所示，矩形的一边在道路AE上，一个顶点在扇形半径OD上．记∠POE＝，求当“矩形草坪”的面积最大时的值．

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网