题目内容
过抛物线y2=2px（p＞0）的焦点F的直线交该抛物线于P、Q两点，弦PQ的中垂线交抛物线的轴于R.求证：|FR|=
|PQ|.
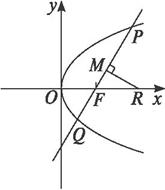
证明：如图所示，设M为PQ的中点，R（x0，0），P（x1，y1），Q（x2，y2）， ∴|FR|=x0- 由题意得|PR|=|QR|,即（x0-x1）2+y12=（x0-x2）2+y22. ∵y22=2px2，y12=2px1，代入上面方程，得（x0-x1）2-（x0-x2）2=2p（x2-x1）,即 ［2x0-（x1+x2）］（x2-x1）=2p（x2-x1）. ∵x1≠x2,∴x0=
.
+p.∴|FR|=
+
=
.
练习册系列答案
随堂1加1导练系列答案
零距离学期系统总复习期末暑假衔接合肥工业大学出版社系列答案
北大绿卡刷题系列答案
五州图书超越假期暑假内蒙古大学出版社系列答案
冲刺名校小考系列答案
黄冈中考考点突破系列答案
初中能力测试卷系列答案
智慧学堂数法题解新教材系列答案
小升初实战训练系列答案
相关题目
过抛物线y2=2px（p＞0）的焦点F的直线l与抛物线在第一象限的交点为A，与抛物线的准线的交点为B，点A在抛物线准线上的射影为C，若
=
，
•
=48，则抛物线的方程为（ ）
| AF |
| FB |
| BA |
| BC |
| A、y2=4x | ||
| B、y2=8x | ||
| C、y2=16x | ||
D、y2=4
|
过抛物线y2=2px（p＞0）的焦点F作直线交抛物线于A、B两点，O为抛物线的顶点．则△ABO是一个（ ）
| A、等边三角形 | B、直角三角形 | C、不等边锐角三角形 | D、钝角三角形 |