��Ŀ����
ij�л����о�����������ÿ�컷����Ⱦ������е����о�����һ�����ۺ���Ⱦָ��f��x����ʱ��x��Сʱ���Ĺ�ϵΪf��x��=|
sin
x+
-a|+2a��x��[0��24]������aΪ�������йصIJ�������a��[
��
]������ÿ����f��x�������ֵ��Ϊ������ۺ���Ⱦָ����������M��a����
������t=
sin
x��x��[0��24]����t��ȡֵ��Χ��
��������M��a���Ľ���ʽ��
����Ϊ��ǿ�Ի�����Ⱦ�����Σ��������涨ÿ����ۺ���Ⱦָ�����ó���2������Ŀǰ�����ĵ��ۺ���Ⱦָ���Ƿꣿ
| 1 |
| 2 |
| �� |
| 32 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 4 |
������t=
| 1 |
| 2 |
| �� |
| 32 |
��������M��a���Ľ���ʽ��
����Ϊ��ǿ�Ի�����Ⱦ�����Σ��������涨ÿ����ۺ���Ⱦָ�����ó���2������Ŀǰ�����ĵ��ۺ���Ⱦָ���Ƿꣿ
��������I���������Һ��������ʣ�����t��ȡֵ��Χ��
��������������ֵ����������M��a���Ľ���ʽ��
�����ɣ���֪M��a�������ֵΪ
����С��2�����ɵó����ۣ�
��������������ֵ����������M��a���Ľ���ʽ��
�����ɣ���֪M��a�������ֵΪ
| 23 |
| 12 |
����⣺������Ϊx��[0��24]������
��[0��
]������sin(
)��[0��1]����t��[0��
]��
������Ϊa��[
��
]������0��a-
��
��
��
����f(t)=|t-(a-
)|+2a=
��
��t��[0��a-
]ʱ��f(t)max=f(0)=3a-
��
��t��[a-
��
]��f(t)max=f(
)=
+a��
��f(0)-f(
)=2a-
��
��
��a��
��f(0)��f(
)��M(a)=f(
)=
+a��
��
��a��
��f(0)��f(
)��M(a)=f(0)=3a-
��
����M(a)=
��
�����ɣ���֪M��a�������ֵΪ
����С��2������Ŀǰ�����ĵ��ۺ���Ⱦָ��û�г��꣮
| ��x |
| 32 |
| 3�� |
| 4 |
| ��x |
| 32 |
| 1 |
| 2 |
������Ϊa��[
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 3 |
| 5 |
| 12 |
| 1 |
| 2 |
����f(t)=|t-(a-
| 1 |
| 3 |
|
��t��[0��a-
| 1 |
| 3 |
| 1 |
| 3 |
��t��[a-
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 6 |
��f(0)-f(
| 1 |
| 2 |
| 7 |
| 6 |
��
| 1 |
| 3 |
| 7 |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 6 |
��
| 7 |
| 12 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
����M(a)=
|
�����ɣ���֪M��a�������ֵΪ
| 23 |
| 12 |
���������⿼�����Ǻ��������ʣ�����������۵���ѧ˼�룬����ѧ�������������������������е��⣮

��ϰ��ϵ�д�
 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д� �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
�����Ŀ
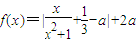 ��x��[{0��24}]������a�������йصIJ�������
��x��[{0��24}]������a�������йصIJ�������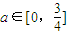 ������ÿ��f��x�������ֵΪ������ۺ���Ⱦָ����������M��a����
������ÿ��f��x�������ֵΪ������ۺ���Ⱦָ����������M��a����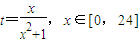 ����t��ȡֵ��Χ��
����t��ȡֵ��Χ�� ��x��[{0��24}]������a�������йصIJ�������
��x��[{0��24}]������a�������йصIJ������� ������ÿ��f��x�������ֵΪ������ۺ���Ⱦָ����������M��a����
������ÿ��f��x�������ֵΪ������ۺ���Ⱦָ����������M��a���� ����t��ȡֵ��Χ��
����t��ȡֵ��Χ��