题目内容
已知![]() ,其中
,其中![]() ,设
,设![]() .
.
(I) 写出![]() ;
;
(II) 证明:对任意的![]() ,恒有
,恒有![]() .
.
【解析】(I)由已知推得![]() ,从而有
,从而有![]()
(II) 证法1:当![]() 时,
时,
![]()
当x>0时, ![]() ,所以
,所以![]() 在[0,1]上为增函数
在[0,1]上为增函数
因函数![]() 为偶函数所以
为偶函数所以![]() 在[-1,0]上为减函
在[-1,0]上为减函
所以对任意的![]()
![]()
![]()
![]()
![]()
![]()
![]()
因此结论成立.
证法2: 当![]() 时,
时,
![]()
当x>0时, ![]() ,所以
,所以![]() 在[0,1]上为增函数
在[0,1]上为增函数
因函数![]() 为偶函数所以
为偶函数所以![]() 在[-1,0]上为减函数
在[-1,0]上为减函数
所以对任意的![]()
![]()
![]()
又因![]()
所以![]()
![]()
![]()
因此结论成立.
证法3: 当![]() 时,
时,
![]()
当x>0时, ![]() ,所以
,所以![]() 在[0,1]上为增函数
在[0,1]上为增函数
因函数![]() 为偶函数所以
为偶函数所以![]() 在[-1,0]上为减函数
在[-1,0]上为减函数
所以对任意的![]()
![]()
![]()
由![]()
![]()
对上式两边求导得
![]()
![]()
∴![]()
因此结论成立.

练习册系列答案
相关题目
 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数. 表示
表示 ;
; ,若
,若 ,试证明数列
,试证明数列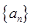 为等比数列,并求数列
为等比数列,并求数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前 ,求
,求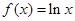 ,
,
 (其中
(其中 是
是 的导函数),求
的导函数),求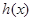 的最大值;
的最大值;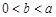 时,求证:
时,求证: ;
;  ,当
,当 时,不等式
时,不等式 恒成立,求
恒成立,求 的最大值
的最大值