Question

设sin²α+sin²β+=sinα·sinβ+sinα+sinβ,求锐角α、β的值.

Answer 1

解析:方法一:(sin²α-sinα+)+(sin²β-sinβ+)+(sin²α-2sinα·sinβ+sin²β)=0,

即(sinα-)²+(sinβ-)²+(sinα-sinβ)²=0.

∴

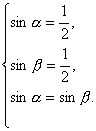
∵α,β为锐角,∴α=β=.

方法二:原等式即sin²α-(sinβ+)sinα+(sin²β-sinβ+)=0.

∵sinα为实数,

∴Δ=(sinβ+)²-4(sin²β-sinβ+)≥0,

即-3sin²β+3sinβ-≥0,

即sin²β-sinβ+≤0,(sinβ-)²≤0,得sinβ=.

代入原方程sin²α-sinα+=0,

(sinα-)²=0,得sinα=.

∴sinα=,sinβ=.

∵α,β为锐角,∴α=β=.