题目内容
 (2012•铁岭模拟)如图,三棱锥P-ABC中,PB⊥底面ABC,PB=BC=CA=4,E为PC的中点,M为AB的中点,点F在PA上,且AF=2FP.
(2012•铁岭模拟)如图,三棱锥P-ABC中,PB⊥底面ABC,PB=BC=CA=4,E为PC的中点,M为AB的中点,点F在PA上,且AF=2FP.(1)求证:BE⊥平面PAC;
(2)求证:CM∥平面BEF;
(3)求三棱锥F-ABE的体积.
分析:(1)利用线面垂直可得线线垂直,进而可得AC⊥平面PBC,即可得线线垂直,再利用线面垂直的判定,即可证得BE⊥平面PAC;
(2)取AF的中点G,AB的中点M,连接CG,CM,GM,利用线线平行证明线面平行,从而可得平面CMG∥平面BEF,利用面面平行的性质,可得线面平行;
(3)证明BE⊥平面PAC,利用等体积转化可求三棱锥F-ABE的体积.
(2)取AF的中点G,AB的中点M,连接CG,CM,GM,利用线线平行证明线面平行,从而可得平面CMG∥平面BEF,利用面面平行的性质,可得线面平行;
(3)证明BE⊥平面PAC,利用等体积转化可求三棱锥F-ABE的体积.
解答:(1)证明:∵PB⊥底面ABC,且AC?底面ABC,∴AC⊥PB …(1分)
由∠BCA=90°,可得AC⊥CB …(2分)
又∵PB∩CB=B,∴AC⊥平面PBC …(3分)
∵BE?平面PBC,∴AC⊥BE …(4分)
∵PB=BC,E为PC中点,∴BE⊥PC …(5分)
∵PC∩AC=C,∴BE⊥平面PAC …(6分)
(2)证明:取AF的中点G,AB的中点M,连接CG,CM,GM,
∵E为PC中点,FA=2FP,∴EF∥CG.…(7分)
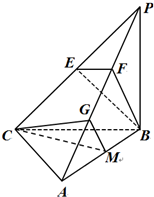 ∵CG?平面BEF,EF?平面BEF,∴CG∥平面BEF.…(8分)
∵CG?平面BEF,EF?平面BEF,∴CG∥平面BEF.…(8分)
同理可证:GM∥平面BEF.
又CG∩GM=G,∴平面CMG∥平面BEF.…(9分)
∵CM?平面CDG,∴CM∥平面BEF.…(10分)
(3)解:由(1)可知BE⊥平面PAC
又PB=BC=4,E为PC的中点,∴BE=2
.
∵S△AEF=
S△PAC=
×
×AC×PC=
…(12分)
∴VF-ABE=VB-AEF=
×S△AEF×BE=
∴三棱锥F-ABE的体积为
.…(14分)
由∠BCA=90°,可得AC⊥CB …(2分)
又∵PB∩CB=B,∴AC⊥平面PBC …(3分)
∵BE?平面PBC,∴AC⊥BE …(4分)
∵PB=BC,E为PC中点,∴BE⊥PC …(5分)
∵PC∩AC=C,∴BE⊥平面PAC …(6分)
(2)证明:取AF的中点G,AB的中点M,连接CG,CM,GM,
∵E为PC中点,FA=2FP,∴EF∥CG.…(7分)
 ∵CG?平面BEF,EF?平面BEF,∴CG∥平面BEF.…(8分)
∵CG?平面BEF,EF?平面BEF,∴CG∥平面BEF.…(8分)同理可证:GM∥平面BEF.
又CG∩GM=G,∴平面CMG∥平面BEF.…(9分)
∵CM?平面CDG,∴CM∥平面BEF.…(10分)
(3)解:由(1)可知BE⊥平面PAC
又PB=BC=4,E为PC的中点,∴BE=2
| 2 |
∵S△AEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
| 2 |
∴VF-ABE=VB-AEF=
| 1 |
| 3 |
| 32 |
| 9 |
∴三棱锥F-ABE的体积为
| 32 |
| 9 |
点评:本题考查线面垂直的判定与性质,考查线面平行,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目