Question

（2012•铁岭模拟）已知函数f（x）=x|x-2|，若存在互不相等的实数a，b，c，使f（a）=f（b）=f（c） 成立，则a+b+c的取值范围是（　　）

• A．[4，3+

  2

  ]
• B．[4，3+

  2

  )
• C．(4，3+

  2

  ]
• D．(4，3+

  2

  )

Answer 1

分析：利用绝对值的几何意义，化简函数解析式，可得函数的图象，利用不相等的实数a，b，c，使f（a）=f（b）=f（c） 成立，a+b=2，2＜c＜1+

2

，从而可得结论．

解答：解：函数f（x）=x|x-2|=

x2-2x=(x-1)2-1，x≥2 -x2+2x=-(x-1)2+1，x＜2

，图象如图所示；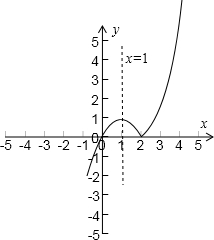
∵x=1时，函数值为1
∴由-x²+2x=1（x≥2），可得x=1+

2

∵不相等的实数a，b，c，使f（a）=f（b）=f（c） 成立，
∴a+b=2，2＜c＜1+

2

∴4＜a+b+c＜3+

2

故选D．

点评：本题考查绝对值函数，考查数形结合的数学思想，考查学生分析解决问题的能力，属于中档题．