题目内容
下列命题:
(1)“若 ,则
,则 ”的逆命题;
”的逆命题;
(2)“全等三角形面积相等”的否命题;
(3)“若 ,则
,则 的解集为R”的逆否命题;
的解集为R”的逆否命题;
(4)“若 为有理数,则
为有理数,则 为无理数”。
为无理数”。
其中正确的命题是 ( )
| A.(3)(4) | B.(1)(3) | C.(1)(2) | D.(2)(4) |
A
解析试题分析:(1)“若 ,则
,则 ”的逆命题是“若
”的逆命题是“若 ,则
,则 ”,显然当取
”,显然当取 时,
时, ,所以是假命题;(2)“全等三角形面积相等”的否命题是“若两个三角形不是全等三角形,则它们的面积不相等”,显然是假命题;(3)“若
,所以是假命题;(2)“全等三角形面积相等”的否命题是“若两个三角形不是全等三角形,则它们的面积不相等”,显然是假命题;(3)“若 ,则
,则 的解集为R”的逆否命题,根据原命题与逆否命题等价,于是当
的解集为R”的逆否命题,根据原命题与逆否命题等价,于是当 时,
时, ,所以不等式
,所以不等式 的解集为R,知其为真命题;(4)“若
的解集为R,知其为真命题;(4)“若 为有理数,则
为有理数,则 为无理数”,因为
为无理数”,因为 是无理数,所以当
是无理数,所以当 为有理数,则
为有理数,则 为无理数,知其为真命题.
为无理数,知其为真命题.
考点:四种命题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
命题“存在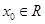 使得
使得 ”的否定是( )
”的否定是( )
A.不存在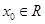 使得 使得 | B.对任意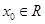 , , |
C.对任意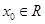 , , | D.存在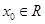 ,使得 ,使得 |
已知函数 ,其中
,其中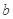 为常数.那么“
为常数.那么“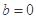 ”是“
”是“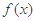 为奇函数”的( )
为奇函数”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
若命题“ 使得
使得 ”为假命题,则实数
”为假命题,则实数 的取值范围是( )
的取值范围是( )
| A.[2,6] | B.[-6,-2] | C.(2,6) | D.(-6,-2) |
设 、
、 是简单命题,则“
是简单命题,则“ 或
或 是假命题” 是 “非
是假命题” 是 “非 为真命题”的 ( )
为真命题”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.非充分非必要条件 |
下列命题中,真命题是( )
A.存在 | B. 是 是 的充分条件 的充分条件 |
C.任意 | D. 的充要条件是 的充要条件是 |
已知命题p:?x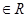 ,
,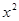 >0,则( )
>0,则( )
A.非p:?x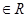 , ,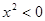 | B.非p:?x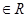 , , |
C.非p:?x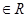 , , | D.非p:?x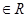 , ,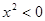 |
给出下列命题:
①命题“ 的否定是:
的否定是: ;
;
②命题“若 ,则
,则 或
或 ”的否命题是“若
”的否命题是“若 ,则
,则 且
且 ”;
”;
③ 、
、 ,
, ;
;
④向量 ,
, 均是单位向量,其夹角为
均是单位向量,其夹角为 ,则命题“
,则命题“ ”是命题“
”是命题“ ”的充要条件.
”的充要条件.
其中正确的命题的个数是( )
| A.4 | B.3 | C.2 | D.1 |
 为假命题,则
为假命题,则 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |