题目内容
设平面内的向量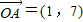 ,
,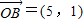 ,
,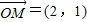 ,点P是直线OM上的一个动点,且
,点P是直线OM上的一个动点,且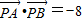 ,求
,求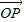 的坐标及∠APB的余弦值.
的坐标及∠APB的余弦值.
【答案】分析:由题意,可设 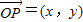 ,再由点P在直线OM上,得到
,再由点P在直线OM上,得到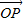 与
与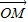 共线,由此共线条件得到x,y之间的关系,代入
共线,由此共线条件得到x,y之间的关系,代入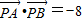 ,解出x,y的值,即可求出
,解出x,y的值,即可求出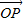 的坐标及
的坐标及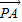 =(-3,5),
=(-3,5),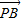 =(1,-1),再由夹角的向量表示公式
=(1,-1),再由夹角的向量表示公式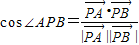 求出∠APB的余弦值
求出∠APB的余弦值
解答:解:(1)由题意,可设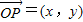 ,∵点P在直线OM上,
,∵点P在直线OM上,
∴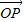 与
与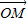 共线,而
共线,而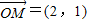 ,
,
∴x-2y=0,即x=2y,有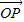 =(2y,y),
=(2y,y),
∵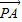 =
=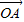 -
-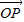 =(1-2y,7-y),
=(1-2y,7-y),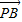 =
=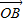 -
-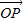 =(5-2y,1-y),
=(5-2y,1-y),
∴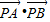 =(1-2y)(5-2y)+(7-y)(1-y),即
=(1-2y)(5-2y)+(7-y)(1-y),即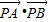 =5y2-20y+12,
=5y2-20y+12,
又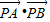 =-8,
=-8,
∴5y2-20y+12=-8,解得y=2,x=4
此时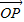 =(4,2),
=(4,2),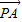 =(-3,5),
=(-3,5),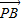 =(1,-1),
=(1,-1),
∴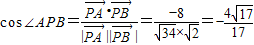
点评:本题考查了向量共线的条件,向量的坐标运算,数量积的坐标表示,向量的模的求法及利用数量积计算夹角的余弦,本题综合性强,运算量大,谨慎计算是正确解题的关键
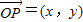 ,再由点P在直线OM上,得到
,再由点P在直线OM上,得到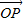 与
与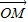 共线,由此共线条件得到x,y之间的关系,代入
共线,由此共线条件得到x,y之间的关系,代入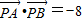 ,解出x,y的值,即可求出
,解出x,y的值,即可求出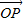 的坐标及
的坐标及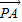 =(-3,5),
=(-3,5),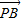 =(1,-1),再由夹角的向量表示公式
=(1,-1),再由夹角的向量表示公式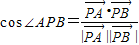 求出∠APB的余弦值
求出∠APB的余弦值解答:解:(1)由题意,可设
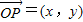 ,∵点P在直线OM上,
,∵点P在直线OM上,∴
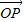 与
与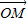 共线,而
共线,而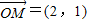 ,
,∴x-2y=0,即x=2y,有
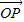 =(2y,y),
=(2y,y),∵
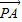 =
=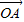 -
-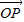 =(1-2y,7-y),
=(1-2y,7-y),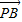 =
=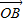 -
-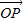 =(5-2y,1-y),
=(5-2y,1-y),∴
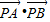 =(1-2y)(5-2y)+(7-y)(1-y),即
=(1-2y)(5-2y)+(7-y)(1-y),即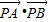 =5y2-20y+12,
=5y2-20y+12,又
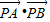 =-8,
=-8,∴5y2-20y+12=-8,解得y=2,x=4
此时
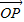 =(4,2),
=(4,2),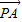 =(-3,5),
=(-3,5),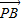 =(1,-1),
=(1,-1),∴
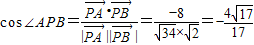
点评:本题考查了向量共线的条件,向量的坐标运算,数量积的坐标表示,向量的模的求法及利用数量积计算夹角的余弦,本题综合性强,运算量大,谨慎计算是正确解题的关键

练习册系列答案
相关题目
 点
点 是直线
是直线 上的一个动点,求当
上的一个动点,求当 取最小值时,
取最小值时, 的坐标及
的坐标及 的余弦值。
的余弦值。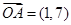 ,
,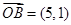 ,
,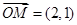 ,点
,点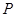 是直线
是直线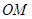 上的一个动点,且
上的一个动点,且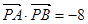 ,求
,求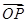 的坐标及
的坐标及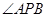 的余弦值.
的余弦值.