题目内容
若函数f(x)=(sinx+cosx)2-2cos2x-m在[0, ]上有零点,则实数m的取值范围为( )
]上有零点,则实数m的取值范围为( )
 ]上有零点,则实数m的取值范围为( )
]上有零点,则实数m的取值范围为( )A.[-1,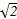 ] ] | B.[-1,1] |
C.[1,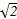 ] ] | D.[-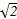 ,-1] ,-1] |
A
f(x)=(sinx+cosx)2-2cos2x-m
="1+sin" 2x-2cos2x-m
="1+sin" 2x-1-cos 2x-m
=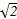 sin(2x-
sin(2x- )-m.
)-m.
∵0≤x≤ ,∴0≤2x≤π,∴-
,∴0≤2x≤π,∴- ≤2x-
≤2x- ≤
≤ ,
,
∴-1≤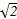 sin(2x-
sin(2x- )≤
)≤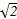 ,
,
故当-1≤m≤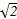 时,f(x)在[0,
时,f(x)在[0, ]上有零点.
]上有零点.
="1+sin" 2x-2cos2x-m
="1+sin" 2x-1-cos 2x-m
=
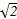 sin(2x-
sin(2x- )-m.
)-m.∵0≤x≤
 ,∴0≤2x≤π,∴-
,∴0≤2x≤π,∴- ≤2x-
≤2x- ≤
≤ ,
,∴-1≤
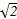 sin(2x-
sin(2x- )≤
)≤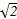 ,
,故当-1≤m≤
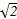 时,f(x)在[0,
时,f(x)在[0, ]上有零点.
]上有零点.
练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 .
. 时,求函数
时,求函数 的单调递增区间;
的单调递增区间; 的内角
的内角 的对应边分别为
的对应边分别为 ,且
,且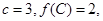 若向量
若向量 与向量
与向量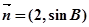 共线,求
共线,求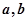 的值.
的值. sin
sin +
+ sinxcosx(x∈R).
sinxcosx(x∈R). 的值;
的值; =1,求sinB+sinC的最大值.
=1,求sinB+sinC的最大值. 对称,则函数的解析式为________.
对称,则函数的解析式为________. (0≤x≤5),点A、B分别是函数y=f(x)图象上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图象上的最高点和最低点. ·
· 的值;
的值;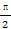 ,1).
,1).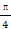 )=
)=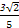 且α∈(0,
且α∈(0, ,x∈R)的图象的一部分如图所示.
,x∈R)的图象的一部分如图所示.
 ]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.



 )(ω>0)和g(x)=3cos(2x+φ)的图象的对称中心完全相同,若x∈
)(ω>0)和g(x)=3cos(2x+φ)的图象的对称中心完全相同,若x∈ ,则f(x)的取值范围是______.
,则f(x)的取值范围是______.