题目内容
求经过点(1,1),倾斜角为135°的直线截椭圆
解:由条件可知直线的参数方程是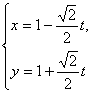 (t为参数),
(t为参数),
代入椭圆方程可得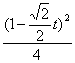 +(1+
+(1+![]() t)2=1,
t)2=1,
即5t2+![]() t+2=0.
t+2=0.
设方程的两实根分别为t1、t2,则由二次方程的根与系数的关系可得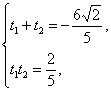 则直线截椭圆的弦长是|t1-t2|=
则直线截椭圆的弦长是|t1-t2|=![]()
=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
求经过点(1,1),倾斜角为135°的直线截椭圆
解:由条件可知直线的参数方程是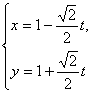 (t为参数),
(t为参数),
代入椭圆方程可得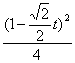 +(1+
+(1+![]() t)2=1,
t)2=1,
即5t2+![]() t+2=0.
t+2=0.
设方程的两实根分别为t1、t2,则由二次方程的根与系数的关系可得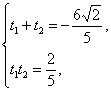 则直线截椭圆的弦长是|t1-t2|=
则直线截椭圆的弦长是|t1-t2|=![]()
=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案