题目内容

求经过点(1,1),倾斜角为135°的直线截椭圆+y2=1所得的弦长.

思路分析：首先可以根据条件写出直线的参数方程(t为参数),代入椭圆的方程可得+(1+t)2=1.这是一个关于t的二次方程,根据参数的几何意义可知所求弦长就是方程两根之差的绝对值.

解：由条件可知直线的参数方程是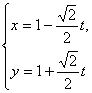(t为参数),代入椭圆方程可得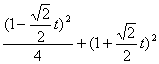=1,即t2+t+1=0.设方程的两实根分别为t1、t2,则由二次方程的根与系数的关系可得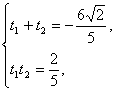则直线截椭圆的弦长是|t1－t2|=.

    误区警示 本题主要使用参数方程中两点的距离公式,易错的地方是:转化参数方程时,计算135°的正弦和余弦值时出错,再者就是距离公式不会灵活使用,而一味地要使用参数的几何意义.

练习册系列答案
相关题目
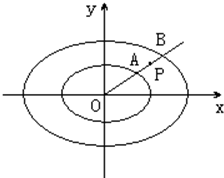精英家教网若椭圆E1：
x2
a
2
1
+
y2
b
2
1
=1和椭圆E2：
x2
a
2
2
+
y2
b
2
2
=1满足
a2
a1
=
b2
b1
=m
 (m＞0)
，则称这两个椭圆相似，m称为其相似比．
（1）求经过点(2，
6
)，且与椭圆
x2
4
+
y2
2
=1相似的椭圆方程；
（2）设过原点的一条射线l分别与（1）中的两个椭圆交于A、B两点（其中点A在线段OB上），
求|OA|+
1
|OB|
的最大值和最小值；
（3）对于真命题“过原点的一条射线分别与相似比为2的两个椭圆C1：
x2
22
+
y2
(
2
)2
=1和C2：
x2
42
+
y2
(2
2
)2
=1交于A、B两点，P为线段AB上的一点，若|OA|、|OP|、|OB|成等差数列，则点P的轨迹方程为
x2
32
+
y2
(
3
2
2
)2
=1”．请用推广或类比的方法提出类似的一个真命题，并给予证明．
已知点Pn（an，bn）（n∈N）满足an+1=anbn+1，bn+1=
bn
1-4
a
2
n
，且点P1的坐标为（1，-1）．
（Ⅰ）求经过点P1，P2的直线l的方程；
（Ⅱ） 已知点Pn（an，bn）（n∈N）在P1，P2两点确定的直线l上，求数列{an}通项公式．
（Ⅲ）在（Ⅱ）的条件下，求对于所有n∈N，能使不等式（1+a1）（1+a2）…（1+an）≥k
1
b2b3…bn+1
成立的最大实数k的值．

(1)求经过点(1,1),且与直线y=2x+7平行的直线的方程;

(2)求经过点(0,2),且与直线y=-3x-5平行的直线的方程;

(3)求经过点(-1,1),且与直线y=-2x+7垂直的直线的方程;

(4)求经过点(-2,-2),且与直线y=3x-5垂直的直线的方程.
求经过点(1,1),倾斜角为135°的直线截椭圆+y2=1所得的弦长.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网