Question

【题目】已知椭圆: 的左右焦点分别 ，过作垂直于轴的直线交椭圆于两点，满足.

（1）求椭圆的离心率.

（2）是椭圆短轴的两个端点，设点是椭圆上一点（异于椭圆的顶点），直线分别与轴相交于两点，为坐标原点，若，求椭圆的方程.

Answer 1

【答案】（1）；（2）

【解析】

（1）在椭圆的方程中，令可得点A的纵坐标，即，然后根据可求得离心率．（2）设，于是可得直线MP和NP的方程，进而得到点R和点Q的横坐标，然后根据可得，于是，故得，从而得到椭圆的方程．

（1）由题意得，点的横坐标为，

又点在椭圆上，

∴，

解得，

∴，

∴，

整理得，

解得或（舍去），

∴．

（2）设，

则直线MP的方程为，

令，得，即点R的横坐标为．

同理可得直线NP的方程为，

令得到Q点的横坐标为

∴，

∴，

∴ ，

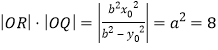∴椭圆的方程为．