题目内容
在 中,角
中,角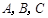 所对的边分别为
所对的边分别为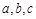 ,且满足
,且满足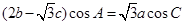 .
.
(1)求角 的大小;
的大小;
(2)现给出三个条件:① ;②
;②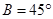 ;③
;③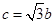 .试从中选出两个可以确定
.试从中选出两个可以确定 的条件,写出你的选项,并以此为依据求出
的条件,写出你的选项,并以此为依据求出 的面积(只需写出一个选定方案即可).
的面积(只需写出一个选定方案即可).
(1) ;(2)选①③,
;(2)选①③, 。
。
解析试题分析:(1)由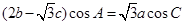 代入正弦定理得:
代入正弦定理得: ,
,
即: ,又
,又 ,
, .又
.又 . 6分
. 6分
(2)方案1:选①②.
由正弦定理 得:
得: .
.
又 ,
, . 12分
. 12分
方案2:选①③.
由余弦定理 得:
得:
∴ ,从而
,从而
 . 12分
. 12分
(选②③,这样的三角形不存在)
考点:正弦定理;余弦定理;三角形的面积公式;三角形内的隐含条件。
点评:熟练掌握三角形内的隐含条件: ;
; 。
。

练习册系列答案
相关题目


 的单调增区间;
的单调增区间; ,求
,求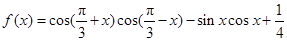
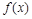 的最小正周期和最大值;
的最小正周期和最大值; 单调递增区间
单调递增区间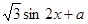 )(
)(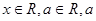 是常数),且
是常数),且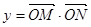 (O为坐标原点)
(O为坐标原点)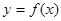 ;
;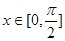 时,
时, 最大值为2013,求a的值.
最大值为2013,求a的值.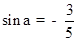 ,且
,且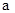 为第三象限角,求
为第三象限角,求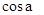 ,
,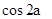 的值
的值
 是
是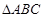 的三个内角,向量
的三个内角,向量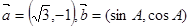 ,且
,且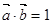 .
.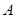 ;
;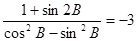 ,求
,求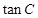 .
.
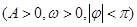 ,在同一周期内,
,在同一周期内,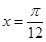 时,
时,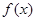 取得最大值
取得最大值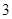 ;当
;当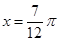 时,
时,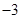 .
. 时,函数
时,函数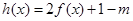 有两个零点,求实数
有两个零点,求实数 的取值范围.
的取值范围.
 化简成
化简成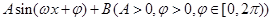 的形式;
的形式;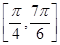 上的最大值和最小值.
上的最大值和最小值. .
.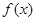 的最小正周期和单调增区间;
的最小正周期和单调增区间;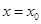 对称,且
对称,且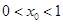 ,求
,求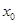 的值.
的值.