题目内容
已知M(1+cos2x,1)、N(1,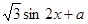 )(
)(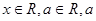 是常数),且
是常数),且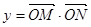 (O为坐标原点)
(O为坐标原点)
(1)求y关于x的函数关系式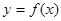 ;
;
(2)若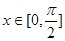 时,
时, 最大值为2013,求a的值.
最大值为2013,求a的值.
(1)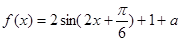 ;(2)
;(2)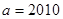 .
.
解析试题分析:(1)因为,M(1+cos2x,1)、N(1,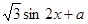 )(
)(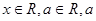 是常数),
是常数),
所以,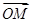 =(1+cos2x,1),
=(1+cos2x,1),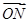 =(1,
=(1,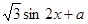 ),
),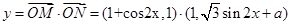 =1+cos2x+
=1+cos2x+ ,
,
故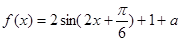 。
。
(2)当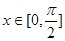 时,
时,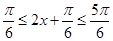 ,所以,
,所以,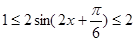
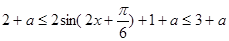 ,从而3+a=2013,a=2010.
,从而3+a=2013,a=2010.
考点:平面向量的坐标运算,和差倍半的三角函数,三角函数的图象和性质。
点评:典型题,在高考题中,往往将平面向量与三角函数综合考查,处理方法是,以向量的运算为起点,建立三角函数式,再利用三角公式化简,运用三角函数的图象和性质进一步解题。

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
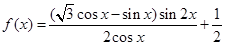 .
.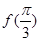 的值;
的值;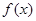 的最小正周期及单调递减区间.
的最小正周期及单调递减区间. 的周期为
的周期为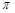 ,图象的一个对称中心为
,图象的一个对称中心为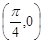 ,将函数
,将函数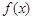 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个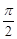 单位长度后得到函数
单位长度后得到函数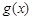 的图象。
的图象。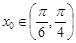 ,使得
,使得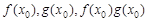 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定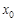 的个数,若不存在,说明理由;
的个数,若不存在,说明理由;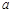 与正整数
与正整数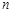 ,使得
,使得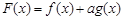 在
在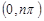 内恰有2013个零点
内恰有2013个零点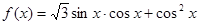 ,
,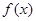 的最小正周期及单调增区间;
的最小正周期及单调增区间; 时,求函数的最值。
时,求函数的最值。
 的值;(2)求
的值;(2)求 的最大值和最小值;
的最大值和最小值;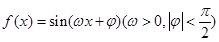 ,在同一个周期内,当
,在同一个周期内,当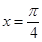 时
时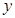 取最大值1,当
取最大值1,当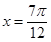 时,
时, ;
; 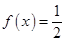 ;求在
;求在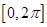 内的所有实数根之和.
内的所有实数根之和. 中,角
中,角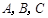 所对的边分别为
所对的边分别为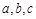 ,且满足
,且满足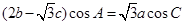 .
.  的大小;
的大小;  ;②
;②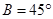 ;③
;③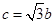 .试从中选出两个可以确定
.试从中选出两个可以确定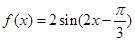
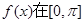 内的单调递增区间;
内的单调递增区间;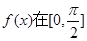 内的值域.
内的值域.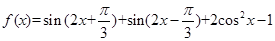 ,
, .
. 求函数
求函数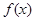 的最小正周期;
的最小正周期; 若函数
若函数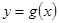 的图像和
的图像和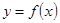 的图像关于直线
的图像关于直线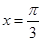 对称,求
对称,求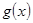 在
在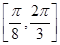 上的最大值和最小值.
上的最大值和最小值.