题目内容
(12分)若定义在R上的函数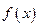 对任意的
对任意的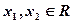 ,都有
,都有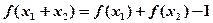 成立,且当
成立,且当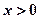 时,
时,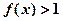 。
。
(1)求证: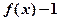 为奇函数;
为奇函数;
(2)求证: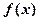 是R上的增函数;
是R上的增函数;
(3)设集合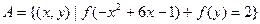 ,
,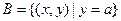 ,且
,且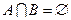 , 求实数
, 求实数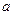 的取值范围。
的取值范围。
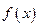 对任意的
对任意的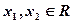 ,都有
,都有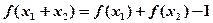 成立,且当
成立,且当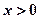 时,
时,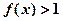 。
。(1)求证:
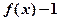 为奇函数;
为奇函数;(2)求证:
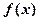 是R上的增函数;
是R上的增函数;(3)设集合
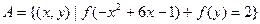 ,
,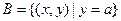 ,且
,且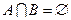 , 求实数
, 求实数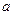 的取值范围。
的取值范围。(1)证明略
(2)证明略
(3)
(2)证明略
(3)

(1)定义在R上的函数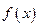 对任意的
对任意的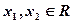 ,
,
都有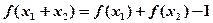 成立
成立
令
令
∴ ,∴
,∴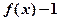 为奇函数
为奇函数
(2)由(1)知: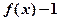 为奇函数, ∴
为奇函数, ∴
任取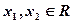 ,且
,且 ,则
,则
∵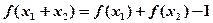
∴
∵当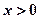 时,
时,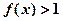 ,
,
∴ ,∴
,∴
∴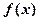 是R上的增函数。
是R上的增函数。
(3)在集合 中
中 由已知条件,有
由已知条件,有

 ,即
,即
在集合 中,有
中,有

 ,则抛物线
,则抛物线 与直线
与直线 无交点
无交点

 ,
, ,
, ,即
,即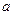 的取值范围是
的取值范围是 。
。
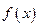 对任意的
对任意的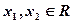 ,
,都有
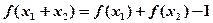 成立
成立令

令

∴
 ,∴
,∴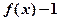 为奇函数
为奇函数 (2)由(1)知:
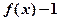 为奇函数, ∴
为奇函数, ∴
任取
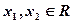 ,且
,且 ,则
,则
∵
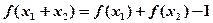
∴

∵当
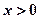 时,
时,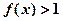 ,
, ∴
 ,∴
,∴
∴
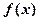 是R上的增函数。
是R上的增函数。 (3)在集合
 中
中 由已知条件,有
由已知条件,有

 ,即
,即
在集合
 中,有
中,有

 ,则抛物线
,则抛物线 与直线
与直线 无交点
无交点
 ,
, ,
, ,即
,即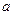 的取值范围是
的取值范围是 。
。
练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 ,则f [f(-2)]=_____________.
,则f [f(-2)]=_____________.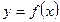 是
是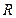 上的偶函数,且
上的偶函数,且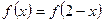 ,如果
,如果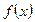 在
在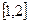 上是减函数,那么
上是减函数,那么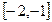 和
和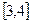 上分别是 ( )
上分别是 ( ) 减函数
减函数  满足
满足
 ___________
___________ 上定义运算:
上定义运算: 若不等式
若不等式 对一切实数
对一切实数 恒成立,则实数
恒成立,则实数 的取值范围为 ( )
的取值范围为 ( )



 ,则
,则 的值是 。
的值是 。 对于任意的
对于任意的 ,都有
,都有
 则
则




 = 。
= 。 的函数
的函数 ,满足
,满足 ;当
;当 时,
时, ,对于
,对于 的值,下列判断正确的是( )
的值,下列判断正确的是( )