题目内容
设△ABC的内角A,B,C所对的边长分别为a,b,c,且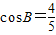 ,b=2.
,b=2.(Ⅰ)当A=30°时,求a的值;
(Ⅱ)当△ABC的面积为3时,求a+c的值.
【答案】分析:(Ⅰ)因为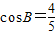 ,可得
,可得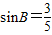 ,由正弦定理求出a的值.
,由正弦定理求出a的值.
(Ⅱ)因为△ABC的面积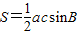 =3,
=3,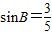 ,可以求得ac=10,再由余弦定理可得a2+c2=20=(a+c)2-2ac,由此求出a+c的值.
,可以求得ac=10,再由余弦定理可得a2+c2=20=(a+c)2-2ac,由此求出a+c的值.
解答:解:(Ⅰ)因为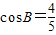 ,所以
,所以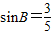 .…(2分)
.…(2分)
由正弦定理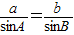 ,可得
,可得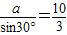 .…(4分)
.…(4分)
所以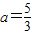 .…(6分)
.…(6分)
(Ⅱ)因为△ABC的面积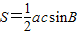 =3,且
=3,且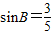 ,
,
所以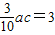 ,ac=10.…(8分)
,ac=10.…(8分)
由余弦定理b2=a2+c2-2accosB,…(9分)
得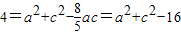 ,即a2+c2=20.…(10分)
,即a2+c2=20.…(10分)
所以(a+c)2 -2ac=(a+c)2 -20=20,
故(a+c)2=40,…(12分)
所以,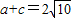 .…(13分)
.…(13分)
点评:本题主要考查正弦定理、余弦定理的应用,同角三角函数的基本关系,属于中档题.
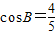 ,可得
,可得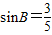 ,由正弦定理求出a的值.
,由正弦定理求出a的值.(Ⅱ)因为△ABC的面积
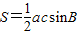 =3,
=3,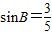 ,可以求得ac=10,再由余弦定理可得a2+c2=20=(a+c)2-2ac,由此求出a+c的值.
,可以求得ac=10,再由余弦定理可得a2+c2=20=(a+c)2-2ac,由此求出a+c的值.解答:解:(Ⅰ)因为
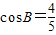 ,所以
,所以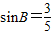 .…(2分)
.…(2分)由正弦定理
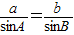 ,可得
,可得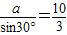 .…(4分)
.…(4分)所以
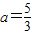 .…(6分)
.…(6分)(Ⅱ)因为△ABC的面积
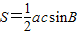 =3,且
=3,且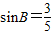 ,
,所以
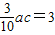 ,ac=10.…(8分)
,ac=10.…(8分)由余弦定理b2=a2+c2-2accosB,…(9分)
得
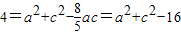 ,即a2+c2=20.…(10分)
,即a2+c2=20.…(10分)所以(a+c)2 -2ac=(a+c)2 -20=20,
故(a+c)2=40,…(12分)
所以,
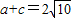 .…(13分)
.…(13分)点评:本题主要考查正弦定理、余弦定理的应用,同角三角函数的基本关系,属于中档题.

练习册系列答案
相关题目