题目内容
下列各组函数是同一函数的是( )①
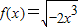 与
与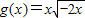 ;
; ②f(x)=x与
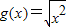 ;
;③f(x)=x与
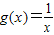 ;
; ④f(x)=x2-2x-1与g(t)=t2-2t-1.
A.①②
B.①③
C.③④
D.①④
【答案】分析:确定函数的三要素是:定义域、对应法则和值域,据此可判断出答案.
解答:解:①f(x)=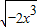 =
=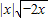 与y=
与y=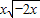 的对应法则和值域不同,故不是同一函数.
的对应法则和值域不同,故不是同一函数.
②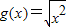 =|x|与f(x)=x的对应法则和值域不同,故不是同一函数.
=|x|与f(x)=x的对应法则和值域不同,故不是同一函数.
③f(x)=x与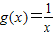 都可化为y=1且定义域是{x|x≠0},故是同一函数.
都可化为y=1且定义域是{x|x≠0},故是同一函数.
④f(x)=x2-2x-1与g(t)=t2-2t-1的定义域都是R,对应法则也相同,而与用什么字母表示无关,故是同一函数.
由上可知是同一函数的是③④.
故选C.
点评:本题考查了函数的定义,明确三要素是判断两个函数是否是同一函数的依据.
解答:解:①f(x)=
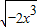 =
=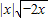 与y=
与y=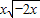 的对应法则和值域不同,故不是同一函数.
的对应法则和值域不同,故不是同一函数.②
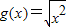 =|x|与f(x)=x的对应法则和值域不同,故不是同一函数.
=|x|与f(x)=x的对应法则和值域不同,故不是同一函数.③f(x)=x与
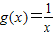 都可化为y=1且定义域是{x|x≠0},故是同一函数.
都可化为y=1且定义域是{x|x≠0},故是同一函数.④f(x)=x2-2x-1与g(t)=t2-2t-1的定义域都是R,对应法则也相同,而与用什么字母表示无关,故是同一函数.
由上可知是同一函数的是③④.
故选C.
点评:本题考查了函数的定义,明确三要素是判断两个函数是否是同一函数的依据.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各组函数中,两个函数是同一函数的是( )
A、f(x)=
| ||||||
B、f(x)=
| ||||||
C、f(x)=(
| ||||||
D、f(x)=x-1,g(x)=
|