题目内容
在数列![]() 中,已知
中,已知![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)![]() 为数列
为数列![]() 的前
的前![]() 项和,求
项和,求![]() ;
;
(3)若总存在正自然数![]() ,使
,使![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
解:(1)解法一:∵![]()
![]() ,
,
∴ ![]() ,
,
∴ 猜想 ![]() ,以下用数学归纳法证明(略)
,以下用数学归纳法证明(略)
解法二: ∵ ![]() , ∴
, ∴![]() , ∴
, ∴ ![]() ,
,
又![]() , ∴ 数列
, ∴ 数列![]() 是以2为公比、以-2为首项的等比数列,
是以2为公比、以-2为首项的等比数列,
∴ ![]() , ∴
, ∴ ![]()
(2)由(1)得:![]() ,∴
,∴![]()
![]() , ∴
, ∴ ![]() ,
,
令![]() , 则
, 则![]() ,
,
两式相减得: ![]()
∴ ![]() , 即
, 即![]() ,∴
,∴![]() =2.
=2.
(3) ∵![]()
令![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 单调递减,
单调递减,
∴ ![]() 单调递增, ∴
单调递增, ∴ ![]() ,
,
∴ ![]() , ∴若总存在正自然数
, ∴若总存在正自然数![]() ,使
,使![]() 成立,则
成立,则![]() .
.
解法二:![]() ,令
,令![]() ,
,
则![]() ,∴数列
,∴数列![]() 单调递减,∴数列
单调递减,∴数列![]() 单调递增,
单调递增,
又![]() ,
,
从而有 ![]() .
.
∴ 若总存在正自然数![]() ,使
,使![]() 成立,则
成立,则![]() .
.

练习册系列答案
相关题目
 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 .
.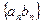 的前
的前 项和
项和 中,已知:
中,已知: .
.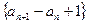 是
是 等比数列.
等比数列. .
.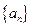 中,已知
中,已知
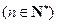 .
. 项和
项和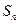 .
. 中,已知
中,已知 且
且 。
。 证明:数列
证明:数列 是等差数列,并求数列
是等差数列,并求数列 求
求 的值。
的值。 中,已知
中,已知 ,
, .
.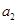 、
、 并判断
并判断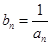 ,求证:
,求证: 为等比数列;
为等比数列;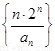 的前n项和
的前n项和 .
.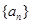 中,已知
中,已知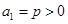 ,且
,且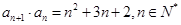 .
.