题目内容
有如下四个命题:
命题①:方程mx2+ny2=1(m>n>0)表示焦点在x轴上的椭圆;
命题②:a+2b=0是直线ax+2y+3=0和直线x+by+2=0互相垂直的充要条件;
命题③:方程mx2-ny2=1(m>n>0)表示离心率大于
的双曲线;
命题④:“全等三角形的面积相等”的否命题.
其中真命题的序号是______.(写出所有真命题的序号)
命题①:方程mx2+ny2=1(m>n>0)表示焦点在x轴上的椭圆;
命题②:a+2b=0是直线ax+2y+3=0和直线x+by+2=0互相垂直的充要条件;
命题③:方程mx2-ny2=1(m>n>0)表示离心率大于
| 2 |
命题④:“全等三角形的面积相等”的否命题.
其中真命题的序号是______.(写出所有真命题的序号)
①方程mx2+ny2=1(m>n>0)表示焦点在y轴上的椭圆,命题①为假命题;
②直线ax+2y+3=0的斜率为-
,直线x+by+2=0的斜率为-b,若两直线垂直,-
•(-b)=-1,即a+2b=.命题②为真命题.
③方程mx2-ny2=1(m>n>0)表示双曲线,离心率为
<
,故命题③是假命题.
④“全等三角形的面积相等”的否命题是“全等三角形的面积不相等”,为假命题.
故答案为:②
②直线ax+2y+3=0的斜率为-
| 2 |
| a |
| 2 |
| a |
③方程mx2-ny2=1(m>n>0)表示双曲线,离心率为
|
| 2 |
④“全等三角形的面积相等”的否命题是“全等三角形的面积不相等”,为假命题.
故答案为:②

练习册系列答案
相关题目
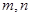 和平面
和平面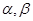 ,有如下四个命题:
,有如下四个命题: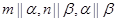 ,则
,则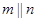 ;
;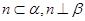 ,则
,则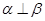 ;
; ,则
,则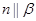 且
且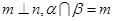 ,则
,则 或
或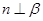 。其中真命题的个数是 .
。其中真命题的个数是 .