题目内容
已知F1、F2是椭圆
+
=1的两个焦点,点P在椭圆上,若△PF1F2是直角三角形,求点P的坐标.
| x2 |
| 9 |
| y2 |
| 4 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据椭圆方程求得c<b,从而判断出点P对两个焦点张角的最大值小于90°,可得直角三角形的直角顶点在焦点处,即可求点P的坐标.
解答:
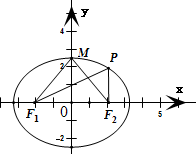 解:设椭圆短轴的一个端点为M,
解:设椭圆短轴的一个端点为M,
∵椭圆
+
=1中,a=3且b=2,∴c=
>b
由此可得∠OMF1<45°,得到∠F1MF2<90°,
∴若△PF1F2是直角三角形,∠PF1F2=90°或∠PF2F1=90°.
P的横坐标为
时,纵坐标为±
,P的横坐标为-
时,纵坐标为±
,
∴P(
,±
)或P(-
,±
).
 解:设椭圆短轴的一个端点为M,
解:设椭圆短轴的一个端点为M,∵椭圆
| x2 |
| 9 |
| y2 |
| 4 |
| 5 |
由此可得∠OMF1<45°,得到∠F1MF2<90°,
∴若△PF1F2是直角三角形,∠PF1F2=90°或∠PF2F1=90°.
P的横坐标为
| 5 |
| 4 |
| 3 |
| 5 |
| 4 |
| 3 |
∴P(
| 5 |
| 4 |
| 3 |
| 5 |
| 4 |
| 3 |
点评:本题给出点P是椭圆上与两个焦点构成直角三角形的点,求点P的坐标.着重考查了椭圆的标准方程、简单几何性质和三角形的面积计算等知识,属于中档题.

练习册系列答案
相关题目
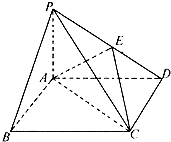 四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,E是侧棱PD的中点.
四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,E是侧棱PD的中点.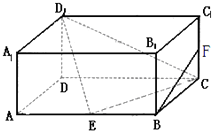 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,E为AB的中点,F为CC1的中点.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,E为AB的中点,F为CC1的中点.