题目内容
若Sn为数列{an}的前n项和且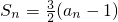 
，求证：数列{an}是等比数列．
解：Sn为数列{an}的前n项和且 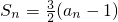，所以an=Sn-Sn-1=
-
，n≥2，
所以an=3an-1，n≥2，满足等比数列的定义，
所以数列{an}是等比数列．
分析：直接利用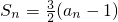，推出Sn-Sn-1=an，n≥2，化简通过等比数列的定义证明即可．
点评：本题是基础题，考查数列前n项和与通项公式的关系，等比数列的定义的应用，考查计算能力．
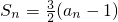，所以an=Sn-Sn-1=-，n≥2，所以an=3an-1，n≥2，满足等比数列的定义，
所以数列{an}是等比数列．
分析：直接利用
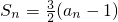，推出Sn-Sn-1=an，n≥2，化简通过等比数列的定义证明即可．点评：本题是基础题，考查数列前n项和与通项公式的关系，等比数列的定义的应用，考查计算能力．
练习册系列答案
相关题目