题目内容
【题目】设函数![]() .
.
(1)求函数![]() 的单调区间及极值;
的单调区间及极值;
(2)若函数![]() 在
在![]() 上有唯一零点,证明:
上有唯一零点,证明:![]() .
.
【答案】(1)![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() ,极小值为
,极小值为![]() ,无极大值(2)见解析
,无极大值(2)见解析
【解析】
(1)求出函数![]() 的定义域以及导数,利用导数求出函数
的定义域以及导数,利用导数求出函数![]() 的单调区间,并由单调性得出函数
的单调区间,并由单调性得出函数![]() 的极值;
的极值;
(2)利用参变量分离法得出关于![]() 的方程
的方程![]() 在
在![]() 上有唯一解,构造函数
上有唯一解,构造函数![]() ,得出
,得出 ,构造函数
,构造函数![]() ,求出该函数的导数,判断导数的符号,得出函数的单调性,求出函数
,求出该函数的导数,判断导数的符号,得出函数的单调性,求出函数![]() 的最小值转化即可。
的最小值转化即可。
(1)![]() 的定义域为
的定义域为![]() ,∵
,∵![]() ,
,
当![]() 时,
时,![]() ,
,![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
∴![]() 有极小值
有极小值![]() ,无极大值,
,无极大值,
故![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() ,极小值为
,极小值为![]() ,无极大值;
,无极大值;
(2)函数![]() 在
在![]() 上有唯一零点,即当
上有唯一零点,即当![]() 时,方程
时,方程![]() 有唯一解,
有唯一解,
∴![]() 有唯一解,令
有唯一解,令![]() ,则
,则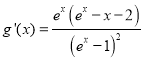
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,故函数
,故函数![]() 为增函数,
为增函数,
又![]() ,
,![]() ,
,
∴![]() 在
在![]() 上存在唯一零点
上存在唯一零点![]() ,则
,则![]() ,且
,且![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上有最小值.ly
上有最小值.ly![]() ,∴
,∴![]() .
.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目