题目内容
15.已知函数f(x)=-x2+2ax+1-a在区间[0,1]上的最大值是3,求实数a的值.分析 先求对称轴,比较对称轴和区间的关系,利用开口向下的二次函数离对称轴越近函数值越大来解题.
解答 解:函数f(x)=-x2+2ax-a+1图象的对称轴为直线x=a,
当a<0时,[0,1]是f(x)的递减区间,f(x)max=f(0)=1-a=3,
∴a=-2;
当a>1时,[0,1]是f(x)的递增区间,f(x)max=f(1)=a=3,
∴a=3;
当0≤a≤1时,f(x)max=f(a)=a2-a+1=3,
解得a=-1(舍去),或a=2(舍去),
所以a=-2或a=3.
点评 此题是个中档题.本题考查了二次函数在闭区间上的最值问题.关于不定解析式的二次函数在固定闭区间上的最值问题,一般是根据对称轴和闭区间的位置关系来进行分类讨论,如轴在区间左边,轴在区间右边,轴在区间中间,最后在综合归纳得出所需结论.

练习册系列答案
相关题目
5.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,过点F的直线与椭圆交于点A,B,若AB中点为(1,-$\frac{1}{2}$),且直线AB的倾斜角为45°,则椭圆方程为( )
| A. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1 | C. | $\frac{2{x}^{2}}{9}$+$\frac{4{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1 |
6.从5人中选3人参加座谈会,其中甲必须参加,则不同的选法有( )
| A. | 12种 | B. | 6种 | C. | 5种 | D. | 4种 |
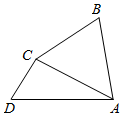 如图四边形ABCD,a,b,c为△ABC的内角A,B,C的对边,且满足b(1+cosA)=a(2-cosB).
如图四边形ABCD,a,b,c为△ABC的内角A,B,C的对边,且满足b(1+cosA)=a(2-cosB).