题目内容
要得到函数y=f'（x）的图象，需将函数f（x）=sinx+cosx（x∈R）的图象（ ）
分析：由f（x）=sinx+cosx=
sin（x+
），可得f'（x）=
sin（x+
），再利用y=Asin（ωx+∅）的图象变换规律得出结论．
| 2 |
| π |
| 4 |
| 2 |
| 3π |
| 4 |
解答：解：f（x）=sinx+cosx=
sin（x+
），∴f'（x）=cosx-sinx=
（
-x）=-
sin（x-
）=
sin（x-
+π）=
sin（x+
），
故将函数f（x）=sinx+cosx（x∈R）的图象向左平移
个单位可得f'（x）=
sin（x+
）的图象，
故选A．
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
| 3π |
| 4 |
故将函数f（x）=sinx+cosx（x∈R）的图象向左平移
| π |
| 2 |
| 2 |
| 3π |
| 4 |
故选A．
点评：本题主要考查两角和差的正弦、诱导公式的应用，y=Asin（ωx+∅）的图象变换规律，属于中档题．
练习册系列答案
相关题目
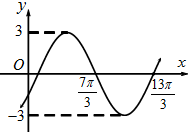函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，