题目内容
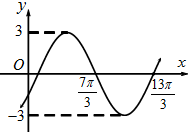 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π | 2 |
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)要得到函数y=f(x)的图象,可由正弦曲线经过怎样的变换得到?
(Ⅲ)若不等式f(x)-m≤2在x∈[0,2π]上恒成立,求实数m的取值范围.
分析:(Ⅰ)利用函数的图象直接得到,A,求出函数的周期,即可求出ω,利用函数经过(
,0),结合φ的范围求出φ的值,即可得到函数f(x)的解析式;
(Ⅱ)由正弦曲线经过初相,变换周期,然后变换振幅,即可推出结果.
(Ⅲ)通过x∈[0,2π],求出相位的范围,求出函数的值的范围,利用不等式f(x)-m≤2在x∈[0,2π]上恒成立,得到m的不等式,求f(x)-2的最大值,即可得到实数m的取值范围.
| 7π |
| 3 |
(Ⅱ)由正弦曲线经过初相,变换周期,然后变换振幅,即可推出结果.
(Ⅲ)通过x∈[0,2π],求出相位的范围,求出函数的值的范围,利用不等式f(x)-m≤2在x∈[0,2π]上恒成立,得到m的不等式,求f(x)-2的最大值,即可得到实数m的取值范围.
解答:解:(Ⅰ)由图象知,A=3,
=
-
=2π⇒T=4π,ω=
=
,
将图象上的点(
,0)代人y=f(x)中,
得φ=2kπ-
,k∈Z,又|φ|<
,
∴φ=-
,
故f(x)=3sin(
x-
).
(Ⅱ)y=sinx的图象向右平移个单位纵坐标不变,得到y=sin(x-
)的图象,
横坐标伸长到原来的2倍,得到y=sin(
x-
),再保持横坐标不变,纵坐标变为原来的3倍,得到f(x)=3sin(
x-
);
(Ⅲ)∵x∈[0,2π],
∴
x-
∈[-
,
],
则sin(
x-
)∈[-
,1],
从而f(x)=3sin(
x-
)∈[-
,3]
不等式f(x)-m≤2在x∈[0,2π]上恒成立等价于:m≥f(x)-2在x∈[0,2π]上恒成立,
而f(x)-2∈[-
,1],
∴m≥1.
| T |
| 2 |
| 13π |
| 3 |
| 7π |
| 3 |
| 2π |
| T |
| 1 |
| 2 |
将图象上的点(
| 7π |
| 3 |
得φ=2kπ-
| π |
| 6 |
| π |
| 2 |
∴φ=-
| π |
| 6 |
故f(x)=3sin(
| 1 |
| 2 |
| π |
| 6 |
(Ⅱ)y=sinx的图象向右平移个单位纵坐标不变,得到y=sin(x-
| π |
| 6 |
横坐标伸长到原来的2倍,得到y=sin(
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
(Ⅲ)∵x∈[0,2π],
∴
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
则sin(
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
从而f(x)=3sin(
| 1 |
| 2 |
| π |
| 6 |
| 3 |
| 2 |
不等式f(x)-m≤2在x∈[0,2π]上恒成立等价于:m≥f(x)-2在x∈[0,2π]上恒成立,
而f(x)-2∈[-
| 7 |
| 2 |
∴m≥1.
点评:本题考查三角函数的解析式的求法,三角函数图象的平移,正弦函数的值域的求法,考查基本知识的应用,分析问题解决问题的能力.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
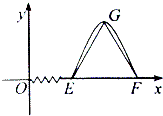 已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是边长为2的正三角形,则f(1)=( )
已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是边长为2的正三角形,则f(1)=( )A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2008)的值等于
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2008)的值等于 函数f(x)=Asin(ωx+?)(其中A>0,ω>0,
函数f(x)=Asin(ωx+?)(其中A>0,ω>0,