题目内容
(2008•徐汇区二模)曲线f(x,y)=0关于直线x-y-2=0对称的曲线方程为
f(y+2,x-2)=0
f(y+2,x-2)=0
.分析:设所求曲线上任意一点A(x,y),由A关于直线x-y-2=0对称的点B(x′,y′)在已知曲线上,根据A与B关于直线x-y-2=0对称建立可得A与B的关系,进而用x、y表示x′,y′,然后代入已知曲线f(x,y)=0,即可求出所求.
解答:解:设所求曲线上任意一点A(x,y),则A(x,y)关于直线x-y-2=0对称的点B(x′,y′)在已知曲线上
∵
∴
因为B(x′,y′)在已知曲线f(x,y)=0上,即f(x′,y′)=0
所以有f(y+2,x-2)=0
故答案为:f(y+2,x-2)=0
∵
|
|
因为B(x′,y′)在已知曲线f(x,y)=0上,即f(x′,y′)=0
所以有f(y+2,x-2)=0
故答案为:f(y+2,x-2)=0
点评:本题主要考查了已知曲线关于直线l对称的曲线的求解,其步骤一般是:在所求曲线上任取一点A求出A关于直线的对称点B,则B在已知曲线上,从而代入已知曲线可求所求曲线,属于中档题..

练习册系列答案
相关题目
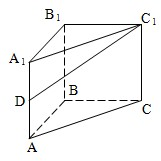 (2008•徐汇区二模)如图直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,∠ABC=90°,AC=2,D是AA1的中点
(2008•徐汇区二模)如图直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,∠ABC=90°,AC=2,D是AA1的中点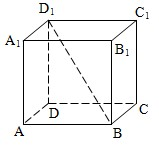 (2008•徐汇区二模)正方体ABCD-A1B1C1D1中,异面直线BD1与AA1所成的角的大小是
(2008•徐汇区二模)正方体ABCD-A1B1C1D1中,异面直线BD1与AA1所成的角的大小是