题目内容
已知|a|=3,|b|=2,a与b的夹角为60°,c=3a+5b,d=ma-3b.
(1)当m为何值时,c与d垂直?
(2)当m为何值时,c与d共线?
解:(1)令c·d=0,则(3a+5b)·(ma-3b)=0,即3m|a|2-15|b|2+(5m-9)a·b=0
解得m= . 故当m=
. 故当m= 时,c⊥d.
时,c⊥d.
(2)令c=λd,则3a+5b=λ(ma-3b) 即(3-λm)a+(5+3λ)b=0,
∵a,b不共线,∴ 解得
解得 故当m=-
故当m=- 时,c与d共线.
时,c与d共线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 :y=2+kt x=1-2t (t为参数)与直线
:y=2+kt x=1-2t (t为参数)与直线 : y=1-2s x=s (s为参数)垂直,则k= 。
: y=1-2s x=s (s为参数)垂直,则k= 。 = .
= . 的图象向左平移
的图象向左平移 个单位,再将所得图象上所有点的横坐标缩短到原来的
个单位,再将所得图象上所有点的横坐标缩短到原来的 倍(纵坐标不变),则所得图象的函数解析式为 ( )
倍(纵坐标不变),则所得图象的函数解析式为 ( ) B.
B.
 D.
D.
 ,面积为
,面积为 ,则扇形的圆心角的弧度数是 .
,则扇形的圆心角的弧度数是 . ,已知
,已知 在
在 时取得极值,则
时取得极值,则 =( )
=( ) 的图象在点
的图象在点 处的切线方程是
处的切线方程是 ,则
,则 _______________.
_______________. +
+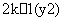 =1表示焦点在y轴上的椭圆,则实数k的取值范围( )
=1表示焦点在y轴上的椭圆,则实数k的取值范围( ) B.(1,+∞) C.(1,2) D.
B.(1,+∞) C.(1,2) D.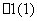
 ,则
,则 等于( )
等于( )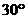 B.
B. C.
C. D.
D.