题目内容
已知
是R上的单调递增函数，则实数
的取值范围为 ( )
| A．(1，＋∞) | B．[4,8) | C．(4,8) | D．(1,8) |
B
解析试题分析：根据函数是R上的单调递增函数，所以
.
考点：分段函数、函数的单调性.
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
已知函数
,则
（ ）
A． | B． | C． | D． |
已知函数
，其中
，若对任意的非零实数
，存在唯一的非零实数
，使得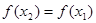
成立，则k的最小值为（ ）
A． | B．5 | C．6 | D．8 |
已知函数
则
( )
A．- | B． | C． | D． |
设函数
，则满足
的x的取值范围是 ( )
A． ，2] | B．[0，2] | C．[1，+ ) | D．[0，+) |
设函数
在
上的导函数为
，在上的导函数为
，若在上，
恒成立，则称函数
在上为“凸函数”.已知当
时，
在
上是“凸函数”，则在上（ ）
| A．既没有最大值，也没有最小值 | B．既有最大值，也有最小值 |
| C．有最大值，没有最小值 | D．没有最大值，有最小值 |
已知
,若
，则x的值是 ( )
| A． | B．1或 | C．1，或± | D．1 |
，则（ ）
A． | B． | C． | D． |
如果函数
在区间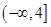
上是减函数，那么实数
的取值范围是（ ）
A． | B． | C． | D． |