题目内容
已知函数
，其中
，若对任意的非零实数
，存在唯一的非零实数
，使得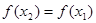
成立，则k的最小值为（ ）
A． | B．5 | C．6 | D．8 |
D
解析试题分析：首先，抛物线的对称轴只能在Y轴右边，所以：
即
………①
这样函数在
上单调递减，所以在
必递增，所以
.……………………………②
根据题意，
时两段函数的函数值应相等，所以
，
所以
.
令
，求导得
.
由此可知：当
时，单调递增；当
时，递减.
所以当
时，
；当
时，
.
所以
或
.又因为，所以.
（另法：也可以利用不等式求
的范围）.
考点：1、分段函数；2、一次函数与二次函数；3、导数的应用；4、不等关系.
练习册系列答案
阅读快车系列答案
相关题目
设函数
仅有一个负零点，则m的取值范围为（ ）
A． | B． |
C． | D． |
已知函数
的定义域是R，则实数
的取值范围是( )
| A．（0,2） | B．（-2,2） | C．[-2,2] | D． |
已知函数
在其定义域上单调递减，则函数
的单调减区间是 （ ）
A． | B． | C． | D． |
已知函数
只有一个零点，则实数m的取值范围是（ ）
A． | B． ∪ |
C． | D． ∪ |
三个数
的大小关系为（ ）
A． | B． |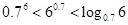
C． | D． |
函数
是幂函数，且在x ∈(0，+∞)上为增函数，则实数m的值是（ ）
| A．-1 | B．2 | C．3 | D．-1或2 |
已知
是R上的单调递增函数，则实数
的取值范围为 ( )
| A．(1，＋∞) | B．[4,8) | C．(4,8) | D．(1,8) |
定义在R上的函数
满足
且
，
，则方程
在区间
上的所有实根之和最接近下列哪个数（ ）
| A． 10 | B． 8 | C． 7 | D． 6 |