题目内容
设A(x1,y1),B(x2,y2)是平面直角坐标系xOy上的两点,先定义由点A到点B的一种折线距离p(A,B)为
对于平面xOy上给定的不同的两点A(x1,y1),B(x2,y2),
(1)若点C(x,y)是平面xOy上的点,试证明 ;
;
(2)在平面xOy上是否存在点c(x,y),同时满足① ;
;
② .
.
若存在,请求所给出所有符合条件的点;若不存在,请予以证明.
【答案】
证明:(1)由绝对值不等式知,



当且仅当 时等号成立,
时等号成立,
即 三点共线时等号成立.
三点共线时等号成立.
(2)当点C(x, y) 同时满足①P +P
+P = P
= P ,②P
,②P =
P
=
P 时,
时,
点 是线段
是线段 的中点.
的中点.  ,
,
即存在点 满足条件。
满足条件。

练习册系列答案
相关题目
设A(x1,y1),B(4,
),C(x2,y2)是右焦点为F的椭圆
+
=1上三个不同的点,则“|AF|,|BF|,|CF|成等差数列”是“x1+x2=8”的( )
| 9 |
| 5 |
| x2 |
| 25 |
| y2 |
| 9 |
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既非充分也非必要 |
设
=(x1,y1),
=(x2,y2),若|
|=2,|
|=3,
•
=-6,则
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| x1+y1 |
| x2+y2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
 +
+ =(a>b>0)上的两点,已知向量m=(
=(a>b>0)上的两点,已知向量m=( ,
, ),n=(
),n=( ,
, ),若m·n=0且椭圆的离心率e=
),若m·n=0且椭圆的离心率e=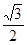 ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.