题目内容
已知向量
,
,
中任意两个都不共线,且
+
与
共线,
+
与
共线,则向量
+
+
= .
| a |
| b |
| c |
| a |
| b |
| c |
| b |
| c |
| a |
| a |
| b |
| c |
考点:平行向量与共线向量
专题:平面向量及应用
分析:利用共线向量定理、平面向量的基本定理即可得出.
解答:
解:∵
+
与
共线,
+
与
共线,
∴存在实数λ,μ使得
+
=λ
,
+
=μ
.
∴
=λ
-
=μ
-
.
∵向量
,
,
中任意两个都不共线,
∴μ=-1,λ=-1.
∴向量
+
+
=
.
故答案为:
.
| a |
| b |
| c |
| b |
| c |
| a |
∴存在实数λ,μ使得
| a |
| b |
| c |
| b |
| c |
| a |
∴
| b |
| c |
| a |
| a |
| c |
∵向量
| a |
| b |
| c |
∴μ=-1,λ=-1.
∴向量
| a |
| b |
| c |
| 0 |
故答案为:
| 0 |
点评:本题考查了共线向量定理、平面向量的基本定理,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
已知复数z=-1+
i,则|z|=( )
| 3 |
| A、2 | ||
| B、3 | ||
| C、4 | ||
D、
|
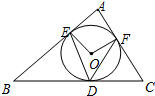 如图,⊙O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
如图,⊙O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )| A、40° | B、55° |
| C、65° | D、70° |

 将连续整数1,2,…,25填入如图所示的5行5列的表格中,使每一行的数字从左到右都成递增数列,则第三列各数之和的最小值为
将连续整数1,2,…,25填入如图所示的5行5列的表格中,使每一行的数字从左到右都成递增数列,则第三列各数之和的最小值为