题目内容
等差数列 中,
中, ,
, ,则
,则 的值是( )
的值是( )
| A.15 | B.30 | C.31 | D.64 |
A
解析试题分析:等差数列 中,序号成等差的项任然成等差数列,故
中,序号成等差的项任然成等差数列,故 成等差,所以
成等差,所以 ,∴
,∴ .
.
考点:等差数列的性质.

练习册系列答案
相关题目
设等差数列 的前
的前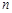 项和为
项和为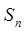 ,
,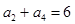 ,则
,则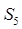 等于( )
等于( )
| A.10 | B.12 | C.15 | D.30 |
已知各项不为0的等差数列 满足
满足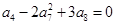 ,数列
,数列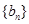 是等比数列,且
是等比数列,且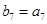 ,则
,则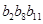 等于( )
等于( )
| A.1 | B.2 | C.4 | D.8 |
等差数列 中的
中的 、
、 是函数
是函数 的极值点,则
的极值点,则 =( )
=( )
A. | B. | C. | D. |
已知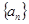 为等差数列,
为等差数列,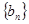 为等比数列,其公比
为等比数列,其公比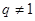 且
且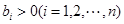 ,若
,若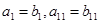 ,则( )
,则( )
A.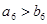 | B.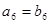 |
C.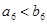 | D.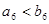 或 或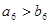 |
各项都是正数的等比数列 的公比
的公比 ,且
,且 成等差数列,则
成等差数列,则 的值为( )
的值为( )
A. | B. |
C. | D. 或 或 |
若数列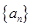 满足
满足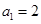 ,
,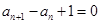
 ,则其通项
,则其通项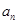 =( )
=( )
A.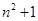 | B.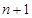 | C.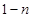 | D.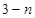 |
三个实数成等差数列,首项是9,若将第二项加2、第三项加20可使得这三个数依次构成等比数列 ,则
,则 的所有取值中的最小值是( )
的所有取值中的最小值是( )
| A.1 | B.4 | C.36 | D.49 |
下面是关于公差d>0的等差数列{an}的四个命题:
p1:数列{an}是递增数列;p2:数列{nan}是递增数列;
p3:数列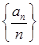 是递增数列;p4:数列{an+3nd}是递增数列.
是递增数列;p4:数列{an+3nd}是递增数列.
其中的真命题为( ).
| A.p1,p2 | B.p3,p4 |
| C.p2,p3 | D.p1,p4 |