题目内容
各项都是正数的等比数列 的公比
的公比 ,且
,且 成等差数列,则
成等差数列,则 的值为( )
的值为( )
A. | B. |
C. | D. 或 或 |
C.
解析试题分析:由 成等比数列,又因为
成等比数列,又因为 成等差数列.所以可得
成等差数列.所以可得 .所以
.所以 ,又因为
,又因为 .所以
.所以 ,所以
,所以 或
或 (舍去)因为等比数列的各项都为正.所以
(舍去)因为等比数列的各项都为正.所以 =
= =
= .故选C.本题是等比数列与等差数列知识的交汇.要分别研究好两个数列.列出一个关于q的等式,题目强调是正项数列所以要舍去一个负的q值.最后的结论是通过整体性来解决这种思想很重要.
.故选C.本题是等比数列与等差数列知识的交汇.要分别研究好两个数列.列出一个关于q的等式,题目强调是正项数列所以要舍去一个负的q值.最后的结论是通过整体性来解决这种思想很重要.
考点:1.等比数列的通项公式.2.等差数列的中项公式.3.整体性来解决数列问题.

练习册系列答案
相关题目
已知等比数列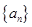 中,各项都是正数,且
中,各项都是正数,且 成等差数列,则
成等差数列,则 ( )
( )
A.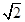 | B. | C. | D. |
在等差数列3, 7, 11 …中,第5项为( )
| A.15 | B.18 | C.19 | D.23 |
等差数列 中,
中, ,
, ,则
,则 的值是( )
的值是( )
| A.15 | B.30 | C.31 | D.64 |
已知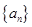 为等差数列,
为等差数列,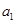 +
+ +
+ =105,
=105, =99,以
=99,以 表示
表示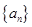 的前
的前 项和,则使得
项和,则使得 达到最大值的
达到最大值的 是( )
是( )
| A.21 | B.20 | C.19 | D.18 |
已知等差数列 的前
的前 项和为
项和为 ,若
,若 且
且 ,则当
,则当 最大时
最大时 的值是( )
的值是( )
| A.8 | B.4 | C.5 | D.3 |
已知等比数列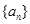 的公比
的公比 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
等差数列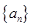 的公差不为零,首项
的公差不为零,首项 ,
, 是
是 和
和 的等比中项,则数列的前
的等比中项,则数列的前 项之和是 ( )
项之和是 ( )
A. | B. | C. | D. |
在等比数列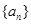 中,
中, 是
是 的等差中项,公比
的等差中项,公比 满足如下条件:
满足如下条件: (
( 为原点)中,
为原点)中, ,
, ,
, 为锐角,则公比
为锐角,则公比 等于( )
等于( )
| A.1 | B.-1 | C.-2 | D. |